Quais as condições para que o produto de dois números naturais seja divisível pela soma dos mesmos? Algebricamente, dados 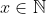 ,
, 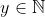 e
e 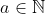 , com
, com 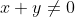 e
e 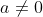 , quando é possível a igualdade
, quando é possível a igualdade
Vamos responder esta pergunta provando que esta equação tem solução em 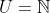 para todo e qualquer valor natural de
para todo e qualquer valor natural de  não nulo. O meio pelo qual faremos isto é resolvendo-a, de fato. Então o formato das soluções nas variáveis
não nulo. O meio pelo qual faremos isto é resolvendo-a, de fato. Então o formato das soluções nas variáveis  e
e  , em função da constante
, em função da constante  , fornecerá as condições de existência da igualdade. Curiosamente, as soluções dependem dos divisores de
, fornecerá as condições de existência da igualdade. Curiosamente, as soluções dependem dos divisores de 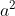 .
.
Começamos fazendo o produto dos meios pelos extremos de (1). Em seguida, isolamos as variáveis no primeiro membro. Chegamos a
Agora faremos um artifício de fatoração, somando e subtraindo do primeiro membro a potência 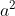 .
.
Colocando em evidência  e
e  e colocando
e colocando 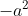 para o segundo membro, temos
para o segundo membro, temos
Por sua vez, colocamos 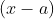 em evidência.
em evidência.
A equação (2) é equivalente a equação (1) com a ressalva 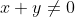 .
.
Concluímos que 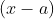 e
e 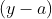 são divisores complementares de
são divisores complementares de 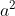 . Designaremos estes divisores por
. Designaremos estes divisores por 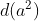 e
e 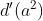 , ou seja,
, ou seja, 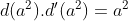 . Assim,
. Assim, 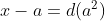 e
e  . Logo,
. Logo,
Exemplo 1. Seja  um primo onde
um primo onde 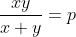 . As soluções naturais para esta equação são geradas pelas igualdades
. As soluções naturais para esta equação são geradas pelas igualdades
Pelo conjunto dos divisores naturais de 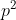 , ou seja,
, ou seja,
temos que
Assim o conjunto solução de 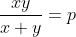 é
é
Com isso, verifica-se que a equação 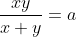 só admite três soluções em
só admite três soluções em 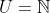 , se
, se  for primo.
for primo.
Exemplo 2. Resolver a equação 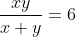 .
.
Temos 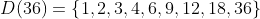 , logo
, logo
E as soluções restantes são os pares com as coordenadas trocadas.
Conclusão: a equação 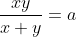 sempre tem soluções em
sempre tem soluções em 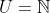 e o número delas é o número de divisores de
e o número delas é o número de divisores de 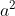 . E ainda, admite as soluções triviais
. E ainda, admite as soluções triviais 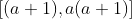 ,
, 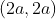 e
e 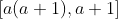 .
.
Observação. A equação 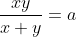 em
em 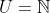 é um caso particular da equação mais geral
é um caso particular da equação mais geral 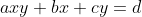 em
em 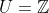 , estudada nos artigos 001 - Uma Equação Diofantina Especial e 006 - Uma Equação Diofantina Especial - II .
, estudada nos artigos 001 - Uma Equação Diofantina Especial e 006 - Uma Equação Diofantina Especial - II .

