Considerem 
relações, onde algumas delas ou todas podem ser funções ou não, definidas pelas equações implícitas
..........................................
Exemplos de relações.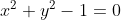 
representa um círculo , ^2-x=0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
representa a figura que estudamos no post 107 e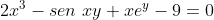 
.
O gráfico da relação-produto
=R_1(x,y)R_2(x,y)...R_k(x,y)=0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
=(y-x)(2x^2+3y^2-7)(-x^2+y+1)=0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
(1)
Fazendo o produto das relações componentes de=0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
, este gráfico também pode ser expressado pelo polinômio do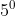 
grau
No que concluimos que se na relação-produto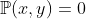
as relações componentes forem todas algébricas ( polinômios ), então o grau de 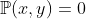será a soma dos graus de cada uma das relações componentes.
Um exemplo prático e artístico. Calculando a equação de cada um dos cinco círculos ( que é uma curva de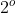
grau ) do símbolo das olimpíadas em relação a um sistema de coordenadas cartesianas. e fazendo a relação-produto, então encontraremos uma única equação de 
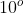grau que esboça este desenho ( considerado plano e sem espessura, é claro ). Neste caso, é interessante escolher o centro do sistema como sendo o centro do círculo preto e, por comodidade, fazer o raio 
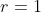para cada círculo.
Para fins de melhor exposição, farei algumas definições.
Definição 1. Contato relativo ao gráfico de uma relação é o ponto onde ocorre auto-interceptação da curva.
O ponto
é um contato no gráfico da relação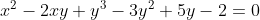 
.
Os pontos e 
são contatos no gráfico da relação-produto (y+x^2-4)=-x^4+8x^2+y^2-16=0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.
Vejam que o gráfico da relação (1) mostrado no primeiro diagrama deste post possui seis contatos.
O gráfico da relação do símbolo das olimpíadas possui oito contatos.
Definição 2. Relação monofuncional é a definida por=y-f(x)=p "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
onde  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
é a lei de definição de uma função, sendo que 
é uma constante real.
Definição 3. Dadas as funções definidas por "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
,  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
,..., "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
, relação polifuncional é a relação- produto definida por
][y-f_2(x)]...[y-f_k(x)]=p "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
onde é uma constante real.
Com os programas modernos de se fazer gráficos, esta conjectura é um dos fatos mais curiosos observáveis na matemática. O que acontece é que os gráficos das relações componentes de=p "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
quando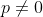 
, se deformam para evitar a existência de contatos, como "água e óleo", não se "misturam", produzindo os mais exóticos gráficos.
Faremos agora uma experiência. Na relação bi-funcional][y-g(x)]=p "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
seja =x^2 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
e =2x-1 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
que é a equação da reta tangente ao gráfico de no ponto  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
. Assim, temos a relação bifuncional(y-2x+1)=p "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
. Se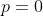 
, o gráfico desta relação produto é
Observem que temos um contato no ponto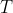
de tangência.
Porém, se
, ou seja, se (y-2x+1)=0,01 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
,vejam o que acontece com este gráfico:
A parábola deixa de ser parábola e a reta deixa de ser reta. As curvas originais se "deformam" para "evitar" o contato. Quando crescer positivamente, ocorre um afastamento gradual entre as duas curvas originais.
Se agora a constante é negativa, vejam o que ocorre no caso de(y-2x+1)=-0,00001 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
:
Da mesma forma, inexistem contatos e se decrescer negativamente, ocorre também um afastamento entre as duas partes da curva.
O gráfico da relação-produto
assume as características individuais de cada relação componente. É lógico pois os pontos que satisfazem são os mesmos que satisfazem =0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
, =0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
ou =0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.
Desta forma, podemos fazer o gráfico de várias relações por intermédio de uma única equação. Mas o conjunto de gráficos sobrepostos de é como se fosse uma única curva que representa a relação-produto.
Exemplo 1. O gráfico de =y-x=0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
representa uma reta. O de =2x^2+3y^2-7=0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
uma elipse e o de =-x^2+y+1=0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
uma parábola. Logo, o gráfico da relação produto =R_1(x,y)R_2(x,y)R_3(x,y)=0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
ou
é o que consta no diagrama:
Fazendo o produto das relações componentes de
No que concluimos que se na relação-produto
Um exemplo prático e artístico. Calculando a equação de cada um dos cinco círculos ( que é uma curva de
Para fins de melhor exposição, farei algumas definições.
Definição 1. Contato relativo ao gráfico de uma relação é o ponto onde ocorre auto-interceptação da curva.
O ponto
Os pontos
Vejam que o gráfico da relação (1) mostrado no primeiro diagrama deste post possui seis contatos.
O gráfico da relação do símbolo das olimpíadas possui oito contatos.
Definição 2. Relação monofuncional é a definida por
Definição 3. Dadas as funções definidas por
onde
Conjectura. Dado a constante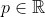 
com 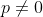então o gráfico da relação produto =R_1(x,y)R_2(x,y)...R_k(x,y)=p "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
não possui contatos. Em decorrência, o gráfico da relação polifuncional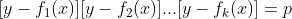 
também não.
Com os programas modernos de se fazer gráficos, esta conjectura é um dos fatos mais curiosos observáveis na matemática. O que acontece é que os gráficos das relações componentes de
Faremos agora uma experiência. Na relação bi-funcional
Observem que temos um contato no ponto
Porém, se
A parábola deixa de ser parábola e a reta deixa de ser reta. As curvas originais se "deformam" para "evitar" o contato. Quando
Se agora a constante é negativa, vejam o que ocorre no caso de
Da mesma forma, inexistem contatos e se
Outro exemplo:
E como último exemplo, o gráfico da relação-produto
Este último comportamento gráfico foi sugerido por Flávio Maia do grupo facebook Física e Matemática e administrador do blog http://ummatematico.blogspot.com.br.
Em outro post, demonstrarei a conjectura deste artigo para a relação bifuncional
