O objetivo do presente artigo é verificar, graficamente e passo a passo, por intermédio de um exemplo, como se constrói um polinômio 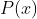 de grau
de grau 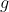 , a partir de
, a partir de 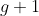 valores iniciais, ou seja,
valores iniciais, ou seja, 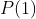 ,
, 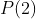 ,...,
,...,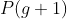 . Veremos também o significado geométrico do coeficiente do termo de maior grau deste polinômio e dos polinômios auxiliares que o formam. Para este fim, introduzimos o conceito de
. Veremos também o significado geométrico do coeficiente do termo de maior grau deste polinômio e dos polinômios auxiliares que o formam. Para este fim, introduzimos o conceito de
Polinômio corretor 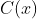 , de grau
, de grau 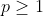 , é aquele que possui as seguintes propriedades.
, é aquele que possui as seguintes propriedades.
a)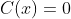 para
para 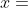
 ,
,  , ...,
, ...,  ;
;
b) para
para 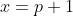 , ou seja, dado um número real
, ou seja, dado um número real 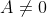 , temos
, temos 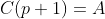 .
.
Logo, tal polinômio tem a forma
a)
b)
Logo, tal polinômio tem a forma
O polinômio corretor 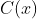 serve para que uma função qualquer
serve para que uma função qualquer  funcione conforme a natureza de uma função
funcione conforme a natureza de uma função 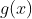 conhecida, conforme as igualdades
conhecida, conforme as igualdades 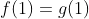 ,
, 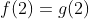 ,....,
,...., , no entanto
, no entanto 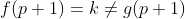 , sendo
, sendo  um valor arbitrariamente escolhido.
um valor arbitrariamente escolhido.
Por exemplo,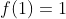 ,
, 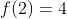 ,
, 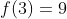 ,
, 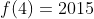 . Sabemos que, para os três primeiros valores,
. Sabemos que, para os três primeiros valores,  funciona como
funciona como 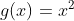 . No entanto para
. No entanto para 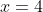 temos a diferença
temos a diferença 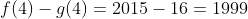 . Logo, fazendo
. Logo, fazendo  no polinômio corretor
no polinômio corretor 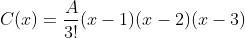 , temos que a função
, temos que a função  é melhor definida por
é melhor definida por
Por exemplo,
De fato, pois
 ,
,
CONSTRUÇÃO DE UM POLINÔMIO DE GRAU g A PARTIR DE VALORES INICIAIS. CONCEITO DE VETOR DE VARIAÇÃO DE GRAU. REPRESENTAÇÃO GEOMÉTRICA.
Dados  ,
, 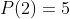 ,
, 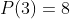 e
e 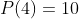 , calcular o polinômio
, calcular o polinômio 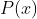 correspondente. E ainda, identificar no gráfico cartesiano os numeradores
correspondente. E ainda, identificar no gráfico cartesiano os numeradores 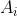 dos coeficientes de todos os polinômios corretores utilizados.
dos coeficientes de todos os polinômios corretores utilizados.
Temos então os pontos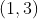 ,
, 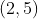 ,
, 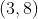 e
e 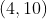 , conforme o diagrama a seguir.
, conforme o diagrama a seguir.
Vejam que , representado pelo ponto
, representado pelo ponto 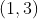 , sugere o polinômio de grau
, sugere o polinômio de grau  ,
,  . Assim, observem no diagrama a seguir que temos
. Assim, observem no diagrama a seguir que temos  e
e 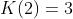 . Mas não queremos o ponto vermelho
. Mas não queremos o ponto vermelho 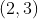 e sim, o ponto azul na mesma vertical
e sim, o ponto azul na mesma vertical 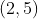 , porque
, porque 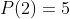 .
.
Temos então os pontos
Vejam que
A diferença das ordenadas de 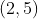 e
e 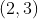 é o módulo de valor
é o módulo de valor 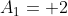 do vetor que indica o sentido da correção. Chamarei vetores deste tipo de vetor de variação de grau. Logo, para alcançarmos o ponto
do vetor que indica o sentido da correção. Chamarei vetores deste tipo de vetor de variação de grau. Logo, para alcançarmos o ponto 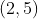 tendo por base o polinômio
tendo por base o polinômio  de grau
de grau  , é necessário somar ao mesmo o polinômio corretor de grau
, é necessário somar ao mesmo o polinômio corretor de grau  ,
,
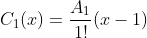
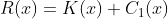 ,
,
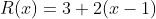
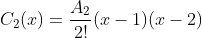
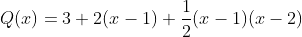
o que da origem a equação da reta
representada no gráfico a seguir.
Embora a reta passe pelos pontos azuis 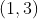 e
e 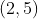 , ela não alcança o ponto azul
, ela não alcança o ponto azul 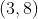 , pois
, pois 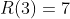 , vide ponto vermelho
, vide ponto vermelho 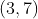 .
.
A diferença das ordenadas de 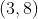 e
e 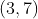 é o módulo de valor
é o módulo de valor  do vetor que indica o sentido da correção. Logo, para alcançarmos o ponto
do vetor que indica o sentido da correção. Logo, para alcançarmos o ponto 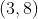 tendo por base o polinômio
tendo por base o polinômio 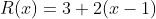 de grau
de grau  , é necessário somar ao mesmo o polinômio corretor de grau
, é necessário somar ao mesmo o polinômio corretor de grau  ,
,
o que dá origem a equação quadrática
representada pela parábola do diagrama a seguir
Agora a parábola abrange os pontos azuis 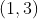 ,
, 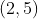 e
e 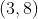 , mas não "pega" o ponto azul
, mas não "pega" o ponto azul 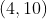 . De fato, pois
. De fato, pois 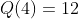 ( ponto vermelho ).
( ponto vermelho ).
A diferença das ordenadas de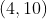 e
e  é o módulo de valor
é o módulo de valor  do vetor que indica o sentido da correção. Logo, para alcançarmos o ponto
do vetor que indica o sentido da correção. Logo, para alcançarmos o ponto 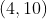 , tendo por base o polinômio
, tendo por base o polinômio 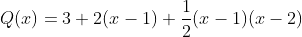 , de grau
, de grau  , é necessário somar ao mesmo o polinômio corretor de grau
, é necessário somar ao mesmo o polinômio corretor de grau 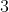 ,
,
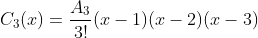
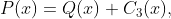

A diferença das ordenadas de
e assim temos polinômio procurado
cujo gráfico é







