DEDICATÓRIA
Dedico esse post a União dos Blogs de Matemática (  ), http://ubmatematica.blogspot.com/, do qual agora sou filiado. Da iniciativa do professor Paulo Sérgio e Kleber Kilhian, a
), http://ubmatematica.blogspot.com/, do qual agora sou filiado. Da iniciativa do professor Paulo Sérgio e Kleber Kilhian, a  prima pela excelência e seriedade, levando aos amantes da matemática uma riqueza de conhecimentos condensados. Eu diria que, se a
prima pela excelência e seriedade, levando aos amantes da matemática uma riqueza de conhecimentos condensados. Eu diria que, se a  tivesse um patrono, sem dúvidas seria o frade Minimita Marin Mersenne (
tivesse um patrono, sem dúvidas seria o frade Minimita Marin Mersenne ( 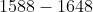 ), um grande difusor de matemática da época.
), um grande difusor de matemática da época.
INTEGRAL NATURAL E SOMATÓRIOS
|
O método de soma exposto a seguir desenvolvi em
No artigo anterior, nós vimos o conceito de derivada natural aplicável a uma sequência qualquer.
Se temos uma sequência  definida por
definida por ) , sua derivada N será definida por
, sua derivada N será definida por
Em contrapartida, se acharmos uma função ) tal que
tal que %3DF(n+1)-F(n)%3Df(n)) , então
, então ) é a INTEGRAL NATURAL ou integral N de
é a INTEGRAL NATURAL ou integral N de ) . Simbolizo
. Simbolizo ) por
por ) . Assim,
. Assim,
A variação de 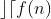 nos limites
nos limites 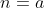 e
e 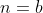 , onde
, onde  e
e  são inteiros positivos com
são inteiros positivos com 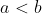 , será representada por
, será representada por
Como a integral N limitada 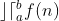 se relaciona com o somatório
se relaciona com o somatório 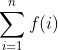 ? É o que veremos a seguir.
? É o que veremos a seguir.
TEOREMA: 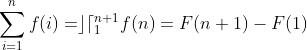
Demonstração: Se existir uma sequência definida por 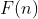 tal que
tal que 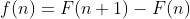 então poderemos somar os termos
então poderemos somar os termos 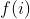 de
de 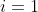 a
a 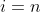 como se segue:
como se segue:
já que todas as parcelas se anulam com exceção da primeira e da última.
Mas, por definição, 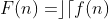 e, portanto,
e, portanto, 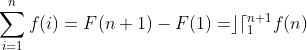
Aplicação 1: Achar a soma de uma progressão geométrica de termo genérico 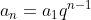 sendo a razão
sendo a razão 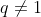 .
.
Solução: multiplicando 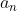 por
por  obtemos
obtemos
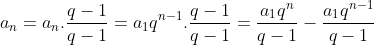
Veja que 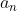 fica no formato
fica no formato 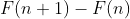 com
com 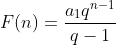
Portanto,
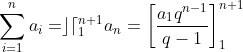
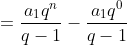
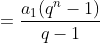
Aplicação 2: Achar a soma dos n primeiros termos da sequência definida por
Solução: Observem que 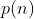 é um polinômio de grau
é um polinômio de grau 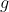 . Para facilitar a soma, teremos que colocar o termo genérico no formato
. Para facilitar a soma, teremos que colocar o termo genérico no formato
E isso já aprendemos no post anterior "Progressão Aritmética de ordem Superior".
Aprendemos também que a derivada N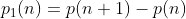 de
de 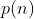 é:
é:
Aprendemos também que a derivada N
Assim, por indução inversa, concluímos que
Logo,
Assim, 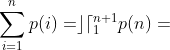
Exemplo. Suponha que 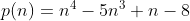 . Pelo triângulo das variações ( ver post anterior ) achamos rapidamente os coeficientes
. Pelo triângulo das variações ( ver post anterior ) achamos rapidamente os coeficientes 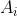 . Se o grau da função polinomial é
. Se o grau da função polinomial é 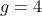 calculamos os
calculamos os 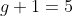 primeiros termos desta função:
primeiros termos desta função:
-11 -30 -59 -68 -3
-19 -29 -9 65
-10 20 74
30 54
24
Pegamos, então, os coeficientes 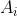 na diagonal da esquerda:
na diagonal da esquerda:
 ,
, 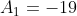 ,
, 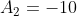 ,
,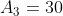 e
e 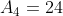
Portanto,
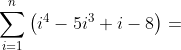

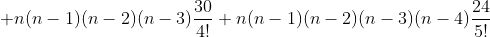
Ou, se preferirem, usando a notação de combinação , temos
Em um futuro post, mostrarei como achar a soma dos  primeiros termos de
primeiros termos de 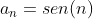 usando a integral N. / N.E: Veja esta matéria em Somatórios Trigonométricos
usando a integral N. / N.E: Veja esta matéria em Somatórios Trigonométricos



