Da Geometria Analítica, sabemos que o gráfico da equação ^2+(y-b)^2=r^2 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
é uma circunferência de centro  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
e raio 
. De posse deste conhecimento, resolveremos os seguintes exercícios. Mostrar que também são circunferências os gráficos das seguintes equações, calcular as coordenadas do centro e o raio de cada uma.
1) 
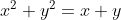
2) 
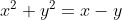
3) 
4)
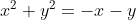
4)
Resolução geral. Inicialmente, provaremos que , dados os números reais
Multiplicando e dividindo por 
os coeficientes de 
e 
e somando ^2+\left(\frac{B}{2}%20\right%20)^2 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
à ambos os membros obtemos
Formados então os
Mas esta é a equação da circunferência de centro  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
e raio ^2+\left(\frac{B}{2}\right)^2+C} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.
Neste contexto, fica bastante simples resolver os exercícios propostos.
1) Comparando
Assim, esta equação é de uma circunferência de centro =\left(\frac{1}{2},\frac{1}{2}\right) "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
que se encontra no primeiro quadrante.
2) Já para 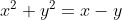, temos o centro=\left(\frac{1}{2},%20-\frac{1}{2}\right) "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
no quarto quadrante.
3) Na equação , temos o centro =\left(-\frac{1}{2},%20\frac{1}{2}\right) "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
situado no segundo quadrante.
4) E por último, temos que na equação
Já os raios destas circunferências são todos iguais, tendo em vista que
Em um mesmo sistema de coordenadas,eis os gráficos das equações estudadas:
Nenhum comentário:
Postar um comentário