Colocaremos, em um mesmo sistema de coordenadas cartesianas, as curvas geradas pela função 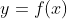 e pela relação
e pela relação 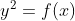 , com o objetivo de visualizar os tipos de transformações que a curva de
, com o objetivo de visualizar os tipos de transformações que a curva de  goza sob um radical, conforme
goza sob um radical, conforme 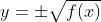 .
.
Podemos, desde já, constatar o seguinte.
1) O domínio da relação 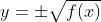 são todos os valores de
são todos os valores de  , onde
, onde 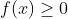 . Na prática, relativo ao esboço de
. Na prática, relativo ao esboço de 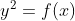 , desprezamos os ramos da curva de
, desprezamos os ramos da curva de 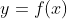 , onde
, onde 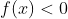 .
.
2) Tendo em vista que 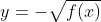 ou
ou 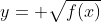 , a curva de
, a curva de 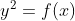 é simétrica em relação ao eixo
é simétrica em relação ao eixo 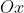 .
.
3) Como 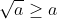 para
para 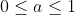 e
e 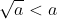 para
para 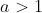 , temos que:
, temos que:
I - Os módulos das ordenadas de 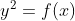 são maiores ou iguais que os módulos das ordenadas de
são maiores ou iguais que os módulos das ordenadas de 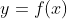 para
para 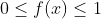 e;
e;
II - Os módulos das ordenadas de 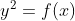 são menores que os módulos das ordenadas de
são menores que os módulos das ordenadas de 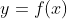 para
para 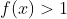 .
.
Nos exemplos gráficos, as curvas de 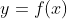 estarão na cor negra e as curvas de
estarão na cor negra e as curvas de 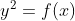 na cor vermelha.
na cor vermelha.
Podemos,então, comprovar os itens 1), 2) e 3) no exemplo elementar onde 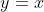 e
e 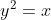 , conforme o gráfico duplo a seguir.
, conforme o gráfico duplo a seguir.
Em alguns casos, é verificado uma simetria também com o eixo 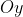 , desde que
, desde que 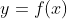 já possua este tipo de simetria. Por exemplo,
já possua este tipo de simetria. Por exemplo, 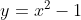 e
e 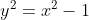 .
.
Informalmente falando, a raiz quadrada desta parábola é uma hipérbole.
Observem que se invertemos os sinais do segundo membro da equação anterior da parábola, ou seja ,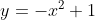 . A curva
. A curva 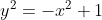 é uma conhecida figura.
é uma conhecida figura.
Informalmente falando, a raiz quadrada desta parábola é uma hipérbole.
Observem que se invertemos os sinais do segundo membro da equação anterior da parábola, ou seja ,
"A raiz quadrada desta parábola é um círculo."
Entramos em um terreno interessante. O aspecto gráfico fechado ( círculo, elipse, ovais) aparece na curva de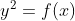 toda vez em que um ponto máximo se encontra entre duas raízes de
toda vez em que um ponto máximo se encontra entre duas raízes de 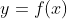 .
.
Exemplos. Dado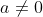 , o gráfico de
, o gráfico de 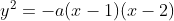 é um círculo para
é um círculo para 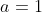 e uma elipse para
e uma elipse para 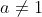 . Vejam os exemplos para
. Vejam os exemplos para 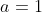 e
e 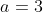 .
.
Entramos em um terreno interessante. O aspecto gráfico fechado ( círculo, elipse, ovais) aparece na curva de
Exemplos. Dado
Sairemos da dimensão das figuras fechadas mais conhecidas. Vejam que a curva vermelha de
enquanto a curva de
Uma curva bastante exótica, que apresentei e analisei no post 107 é gerada pela equação
A relação transcendente interessante e mais básica, cujo gráfico apresenta ovais, é
Por outro lado, até uma relação formada por uma função descontínua como
Geralmente, os módulos das ordenadas das funções exponenciais tem um ímpeto de crescer "agressivamente" para o infinito. Mas essa "ânsia" pode ser contida numa curva fechada por intermédio da relação 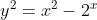 .
.













