Aritmética de Diofanto ( sec III ) Pierre de Fermat (1601-1665)
A solução da equação diofantina
Equação diofantina é aquela de natureza polinomial, de coeficientes inteiros, que possui mais de uma variável e só se buscam soluções inteiras. São também chamadas de indeterminadas, mas, se restringirmos o conjunto-universo das soluções, é possível, em algumas, vislumbrar um algoritmo que permita achar todas as soluções. Não é a toa que só se busquem soluções inteiras. Exemplos de equações diofantinas:
Essas equações levam este nome devido aos estudos de Diofanto de Alexandria que viveu provavelmente na segunda metade do século III. Sua obra principal, Arithmetica de Diofanto, inspirou o jurista e matemático amador francês Pierre de Fermat 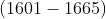 na sua pesquisa sobre a equação
na sua pesquisa sobre a equação 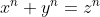 , com
, com 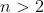 e
e  ,
,  e
e 
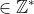 . Este detetive dos números rotulou-a de insolúvel ( Último Teorema de Fermat ) e sua demonstração original, conhecida como o "Santo Grall" da Teoria dos Números, talvez esteja para sempre perdida na névoa do tempo.
. Este detetive dos números rotulou-a de insolúvel ( Último Teorema de Fermat ) e sua demonstração original, conhecida como o "Santo Grall" da Teoria dos Números, talvez esteja para sempre perdida na névoa do tempo.
Como se pode ver, o grau de uma equação diofantina é o grau de seu monômio de maior grau.
Assim, a equação 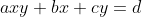 é uma equação diofantina do segundo grau incompleta devido ao monômio
é uma equação diofantina do segundo grau incompleta devido ao monômio 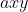 que é do segundo grau. É por isso que existe o pré-requisito
que é do segundo grau. É por isso que existe o pré-requisito 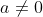 de forma a garantir o grau desta equação.
de forma a garantir o grau desta equação.
Vamos ver, agora, uma série de exemplos usando meu método de resolução. Em todos os exemplos, considere o conjunto solução como sendo todos os pares 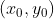 , com
, com 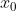 e
e 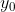
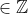 que satisfaçam a igualdade
que satisfaçam a igualdade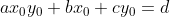 .
.
1) 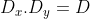 ou seja,
ou seja, 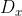 e
e 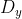 são divisores inteiros e complementares de
são divisores inteiros e complementares de 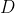 ;
;
2) Se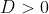 ,
, 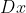 e
e 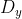 têm o mesmo sinal;
têm o mesmo sinal;
2) Se
Se 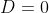 ,
, 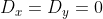 ;
; 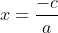 e
e 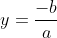 ;
;
Se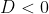 ,
, 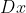 e
e 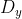 têm sinais opostos.
têm sinais opostos.
Se
3) A equação terá soluções inteiras se  dividir simultaneamente
dividir simultaneamente 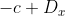 e
e 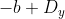 ;
;
4) Se 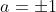 , o número de soluções
, o número de soluções 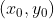 será o número de divisores inteiros de
será o número de divisores inteiros de 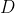 .
.
EXEMPLO 1
Resolver a equação 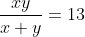 , com
, com 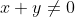
Resolução:
Resolução:
A equação é equivalente à 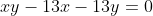 , com a ressalva
, com a ressalva 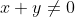 .
.
Dados: 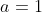 ,
, 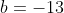 ,
, 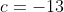 e
e 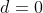
Observem que foi descartado o par 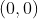 tendo em vista que
tendo em vista que 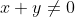 . No entanto, se a equação original fosse
. No entanto, se a equação original fosse 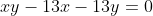 , este par também seria solução.
, este par também seria solução.
EXEMPLO 2
Resolução:
Notem que ocorreram 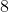 soluções que é o número de divisores inteiros de
soluções que é o número de divisores inteiros de 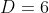 . Isto acontece toda vez que
. Isto acontece toda vez que 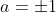 . Disto decorre que, neste caso, se
. Disto decorre que, neste caso, se 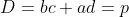 , com
, com  primo, então a equação terá apenas
primo, então a equação terá apenas 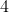 soluções inteiras , porque
soluções inteiras , porque 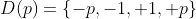 .
.
EXEMPLO 3
Dados
EXEMPLO 4
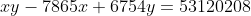
Resolução:
EXEMPLO 5
Resolução:
Esta equação ilustra o caso em que 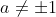 . [ Ver 3) ].
. [ Ver 3) ].
A equação terá soluções inteiras se 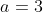 dividir simultaneamente
dividir simultaneamente 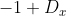 e
e 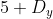 .
.
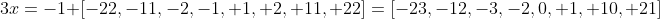
Verifica-se, no último resultado, que os pares correspondentes na mesma coluna, ambos divisíveis por 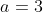 são:
são:
E, portanto, as únicas quatro soluções inteiras da equação 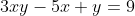 estão contidas em
estão contidas em
SUGESTÃO DE EXEMPLOS INTERATIVOS
1) Achar todos os casos de comprimentos inteiros em que a soma numérica da área de um retângulo com seu perímetro é 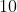 . É equivalente a resolver a equação
. É equivalente a resolver a equação 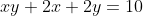 considerando-se apenas os pares positivos.
considerando-se apenas os pares positivos.
2) Dados duas PA de primeiros termos 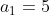 e
e 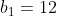 e razões
e razões 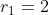 e
e 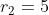 , respectivamente, achar os índices
, respectivamente, achar os índices  de forma que
de forma que 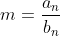 seja inteiro. É equivalente a resolver a equação
seja inteiro. É equivalente a resolver a equação 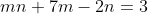 .
.
3) Achar os pontos inteiros da hipérbole gerada por 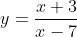 . Resolver a equação
. Resolver a equação 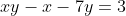 .
.
4) Agora, vamos ver uma aplicação que não é muito prática, mas não deixa de ser curiosa. Resolver, em 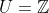 , a equação cúbica de coeficientes inteiros
, a equação cúbica de coeficientes inteiros 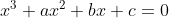 . Basta substituir
. Basta substituir 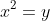 para termos a equação diofantina
para termos a equação diofantina 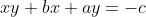 . O problema é que inúmeras soluções estranhas aparecem. Além do mais, é mais fácil achar as raízes inteiras inspecionando os divisores de
. O problema é que inúmeras soluções estranhas aparecem. Além do mais, é mais fácil achar as raízes inteiras inspecionando os divisores de  do que os divisores de
do que os divisores de 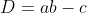 .
.
Fonte Histórica:
O Romance das Equações Algébricas - A história da Álgebra, de Gilberto G. Garbi, Editora MAKRON Books, 1997.



Olá, Aloísio Teixeira!!!!
ResponderExcluirBom dia!!!!
Parabéns, pela sua invenção matemática, amigo!!!
Até agora, eu não tinha visto nem vi tal método resolutivo e o achei... fantástico!!!
O meu blog, tem algumas invenções matemáticas minhas, ou seja: sou metido a pesquisador da ciência dos números, também. Mas, a minha maior invenção nesse campo (que eu a considero como tal) será lançada nesse ano de 2012, para facilitar e agilizar o trabalho com as equações polinomiais com qualquer grau e de coeficientes reais. No momento, lá em meu blog na página intitulada... Desafios, podemos ter uma noção do poder de fogo dessa minha criação!!!
Olha, eu vou resolver umas coisas pedentes no meu sistema de hardware e software, mas gostaria de brevemente, colocar o seu logo (ainda , não tem um?) em meu blog, estabelecer assim uma parceria entre os blogs. Está de acordo????
Também, quero cumprimentá-lo por ter filiado o seu blog à UBM, o que para mim, mostra que o indivíduo é de fato, interessado e atuante nos setores científicos, organizado, cooperativo e nem um pouco... egoísta!!!!
Até breve!!!!
Um abraço!!!!!
Bom dia, Francisco Valdir!
ExcluirObrigado pelas considerações!!
Pra mim será uma honra e um prazer em tê-lo como parceiro.
Seu trabalho em equações polinomiais muito me interessa pois gosto deste assunto. Vou dar uma olhada na sua seção Desafios.
Como vê, a UBM está cumprindo seu papel de integrar a comunidade entusiástica da matemática, para amizade, troca de idéias, sugestões e engrandecimento desta disciplina.
Percebo em suas palavras, amigo Valdir, que tem uma grande energia criadora e como sei que esta qualidade reflete no seu blog, vou vasculhá-lo, dissecá-lo ( com sua permissão ) na busca de inovações.
Como disse Albert Einstein: "A imaginação é mais importante que o conhecimento". É claro que isto é uma meia verdade porque a imaginação é tão importante quanto o conhecimento, onde uma não serviria a nada sem a outra.
Até logo e outro abraço!!
ai cara ,eu também desenvolvi uma solução para esse tipo de equação, mas baseava se na demonstração das equações diofantinas lineares com três incógnitas, mas seu método parece ser muito bom.
ResponderExcluiragora quero te propor um desafio:
a equação diofantina ax+by+cxy=d admite pelo menos uma solução inteira se (a) for diferente de 1,(b)e (c) forem consecutivos e ainda (c)for maior que (b.
valeu!!
Oi, anônimo, se desejar, mande seu método pelo e-mail para eu dar uma olhada.
ResponderExcluirObrigado pela visita.