Considere
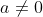
,
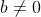
,

e

todos
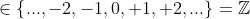
, com
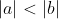
.
Recordem que o máximo divisor comum ( MDC ) de

e

, simbolizado por
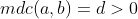
, é o maior dos divisores comuns de

e

.
Ex:
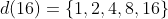
e
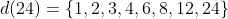
Os divisores comuns de
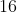
e
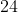
são
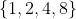
e o maior deles é
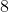
. Logo,
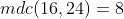
.
O que proponho é o seguinte.
DEMONSTRAR que a combinação
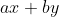
é sempre múltiplo inteiro de
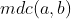
.
Ou, em outras palavras, se
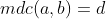
, mostrar que
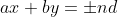
, para
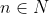
.
Demonstração: Seja

o conjunto que contêm todos os valores não-negativos de
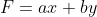
, ou seja,
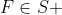
onde
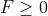
.

é o primeiro elemento positivo de

, portanto, existem

e

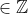
, tal que
E
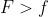
representa qualquer outro elemento de S+:
Se dividirmos F por f podemos ter um quociente
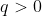
e um resto
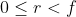
.
Assim,
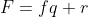
O próximo passo agora é mostrar que o resto

também
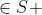
. Vejamos,
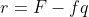
, mas
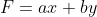
e
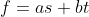
e substituindo estes valores no primeiro,
Desta forma, existem

e

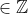
onde

e conclui-se que
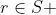
.
No entanto
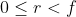
e, por hipótese,

é o primeiro elemento positivo de
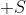
. Logo,
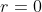
.
O fato de
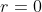
nos traz três importantes consequências:
1ª - Qualquer elemento
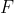
de

é múltiplo do primeiro elemento positivo

porque
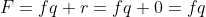
;
2ª - Como
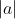
e
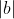
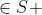
, eles também são múltiplos de

o que é a mesma coisa em dizer que

é um
divisor comum de de

e

;
3ª - Seja
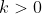
qualquer outro divisor comum de de

e

. Por
concuímos que

divide

e assim,
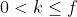
, ou seja,

é maior que todos os outros divisores comuns.
Portanto,
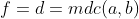
e
Para os valores de
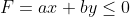
a prova é trivial. Basta considerar o módulo de
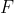
.
Logo,
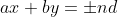
, para
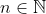
.
Fonte: Teoria dos Números, de
Salahoddin Shokranian,
Marcus Soares,
Hemar Godinho;
Editora UNB, 1998.
 ,
, 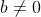 ,
,  e
e  todos
todos 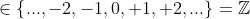 , com
, com 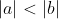 .
. e
e  , simbolizado por
, simbolizado por 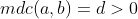 , é o maior dos divisores comuns de
, é o maior dos divisores comuns de  e
e  .
.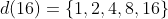 e
e 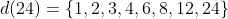
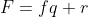
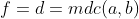 e
e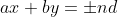 , para
, para 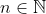 .
.

Nenhum comentário:
Postar um comentário