Seja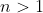 
um número natural e considere 
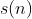a soma dos divisores positivos 
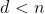do mesmo.
Se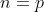 
primo, então 
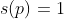porque o único divisor 
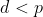é 1 .
De modo geral, dado um 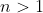qualquer, três possibilidades podem ocorrer:
1) 
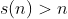e 
é chamado de número abundante;
Ex: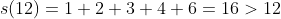 
2) 
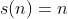e é chamado de NÚMERO PERFEITO;
Ex: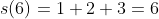 
3) 
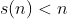e é chamado de número deficiente.
Como foi visto acima, todo número primo é um número deficiente: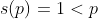 
mas existem números compostos que são deficientes, como por exemplo
Vamos nos concentrar agora nos números perfeitos que são os objetos deste estudo.
Os números perfeitos são extremamente raros. Só para terem uma ideia, o primeiro número perfeito é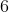 
, o segundo é 
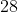, o terceiro já pula para 
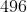, o quarto alça voo para 
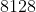e o quinto está na casa dos milhões! Hoje em dia se conhece pouco mais que 
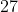números perfeitos e todos são pares. Mesmo porque não se sabe se número perfeito ímpar exista...
Realmente, essa é uma bela parte da Teoria dos Números. E antiga também.
Euclides de Alexandria ( 300 A.C. ) foi o primeiro a dar um tratamento formal sobre o assunto. Ele desconfiou que os números perfeitos tem algo a haver com a potência de 
. E é dele o processo de achar números perfeitos pares. Então porque se conhecem pouco mais que 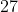? É porque, na verdade, o processo depende de se achar também um número primo muito grande.
Mas vamos a teoria. Para acharmos números perfeitos teremos que estudar a seguinte função aritmética:
Por exemplo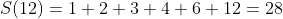 
Observem que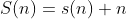 
.
Para 
primo, temos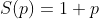 
.
É interessante o cálculo de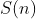 
quando é uma potência de um primo. Os divisores da potência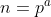 
com primo e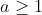 
são 
,,
,
,...,
,
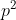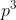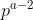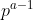e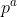 
. Ora, isso são os 
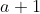termos de uma PG de primeiro termo e razão . Portanto,
A função aritmética 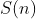tem uma propriedade muito importante que diz que se 
,
,...,
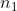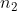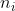são todos primos entre si, dois a dois ( ou seja, cada um não tem fatores primos comuns com qualquer outro considerado nessa seleção ), então
E isso é ideal para calcularmos a soma dos divisores de um número qualquer. Basta fatorá-lo. Se queremos saber a soma dos divisores de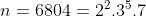 
, já que cada primo de um fator não aparece nos outros fatores, usamos essa propriedade:
Euclides observou que é mais fácil achar números perfeitos pares do que ímpares. Temendo que os perfeitos ímpares não existissem, passou a investigar os números da forma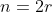 
que possam ser perfeitos. Existindo a possibilidade de 
ainda ser par, ele reescreveu na forma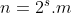 
, com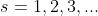 
de forma que 
não contenha nenhum fator , o que é a mesma coisa em dizer que, por hipótese, é ímpar. Depois, para arredondamento de cálculos algébricos, sentiu-se a necessidade de substituir 
por 
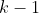com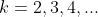 
. Portanto, foram sondados os números pares da forma 
.
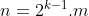Se for perfeito, qual é a natureza do misterioso número ímpar ? É isso que vamos investigar agora.
Como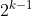 
e não tem fatores primos em comum, temos
Mas, sendo perfeito 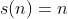e como
Igualando os resultados ( 1 ) e ( 2 ):
Nesse contexto, percebe-se que, como e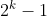 
são ímpares, então o primeiro é divisível pelo segundo. Seja 
o resultado desta divisão. Assim,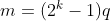 
. Substituindo em ( 3 ):
Te tudo, tiramos o seguinte:
1ª -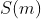 
é a soma de TODOS os divisores do número ímpar ;
2ª - Sabemos que é divisor de ;
3ª - De 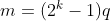, concluímos que é também divisor de ;
4ª - Nosso último resultado diz que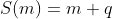 
e, portanto, possui apenas divisores;
5ª - Conclusão: é primo! e seus divisores são e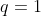 
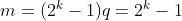
Logo, 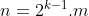será perfeito toda vez que 
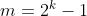for um número primo.
E a forma geral dos número perfeitos pares fica:
Verifica-se que 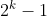é primo para 
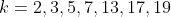o que, aplicados em 
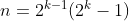, nos fornece os 
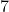primeiros números perfeitos:
Fonte: - Funções Aritméticas - Números Notáveis, de Edgard de Alencar Filho, Editora Nobel,1988
- Cálculo com Geometria Analítica - Volume 1, de George F.Simmons, Editora McGraw-Hill,1967
- História da Matemática, de Carl B.Boyer, Editora Edgard Blücher LTDA, 1974.
Olá Aloisio, o seu blog começou muito bem com muitos assuntos interessantes.Gosto de Teoria dos Números e de vez em quando eu publico alguns assuntos também. Tenho algumas dicas para o seu blog, por exemplo, use a fonte Verdana ao invés de Times New Roman, pois ela é mais arrendondada e facilita a leitura. Outra dica também é criar uma lista de blogs e colocá-la no canto direito do seu blog. No meu, ela está com o título de Blogs interessantes e bom desta lista que você pode fazer parcerias links. Outra dica é classificar os posts com marcadores, tais como: Álgebra Elementar, Teoria dos Números, Matemática Discreta, Cálculo, etc.
ResponderExcluirDevido a qualidade dos seus posts, passei a ser um seguidor também.
Oi, Prof, obrigado pelas dicas. Elas vinheram em boa hora. Agora que stou começando a explorar os recursos do blog. Em relação aos marcadores, utilizarei quando tiver assuntos mais diferenciados. Valeu!
ResponderExcluir