DEDICATÓRIA
Dedico esse post a União dos Blogs de Matemática (  ), http://ubmatematica.blogspot.com/, do qual agora sou filiado. Da iniciativa do professor Paulo Sérgio e Kleber Kilhian, a
), http://ubmatematica.blogspot.com/, do qual agora sou filiado. Da iniciativa do professor Paulo Sérgio e Kleber Kilhian, a  prima pela excelência e seriedade, levando aos amantes da matemática uma riqueza de conhecimentos condensados. Eu diria que, se a
prima pela excelência e seriedade, levando aos amantes da matemática uma riqueza de conhecimentos condensados. Eu diria que, se a  tivesse um patrono, sem dúvidas seria o frade Minimita Marin Mersenne (
tivesse um patrono, sem dúvidas seria o frade Minimita Marin Mersenne (  ), um grande difusor de matemática da época.
), um grande difusor de matemática da época.
INTEGRAL NATURAL E SOMATÓRIOS
|
O método de soma exposto a seguir desenvolvi em
No artigo anterior, nós vimos o conceito de derivada natural aplicável a uma sequência qualquer.
Se temos uma sequência  definida por
definida por ) , sua derivada N será definida por
, sua derivada N será definida por
Em contrapartida, se acharmos uma função ) tal que
tal que %3DF(n+1)-F(n)%3Df(n)) , então
, então ) é a INTEGRAL NATURAL ou integral N de
é a INTEGRAL NATURAL ou integral N de ) . Simbolizo
. Simbolizo ) por
por ) . Assim,
. Assim,
A variação de 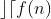 nos limites
nos limites 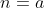 e
e 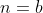 , onde
, onde  e
e  são inteiros positivos com
são inteiros positivos com 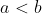 , será representada por
, será representada por
Como a integral N limitada 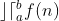 se relaciona com o somatório
se relaciona com o somatório 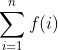 ? É o que veremos a seguir.
? É o que veremos a seguir.
TEOREMA: 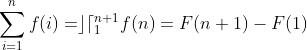
Demonstração: Se existir uma sequência definida por 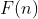 tal que
tal que 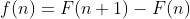 então poderemos somar os termos
então poderemos somar os termos 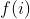 de
de 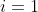 a
a 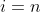 como se segue:
como se segue:
já que todas as parcelas se anulam com exceção da primeira e da última.
Mas, por definição, 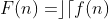 e, portanto,
e, portanto, 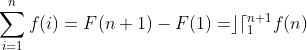
Aplicação 1: Achar a soma de uma progressão geométrica de termo genérico 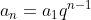 sendo a razão
sendo a razão 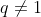 .
.
Solução: multiplicando 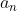 por
por  obtemos
obtemos
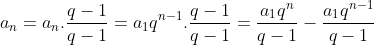
Veja que 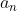 fica no formato
fica no formato 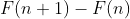 com
com 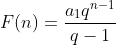
Portanto,
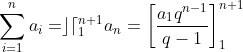
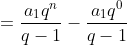
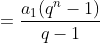
Aplicação 2: Achar a soma dos n primeiros termos da sequência definida por
Solução: Observem que 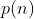 é um polinômio de grau
é um polinômio de grau 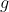 . Para facilitar a soma, teremos que colocar o termo genérico no formato
. Para facilitar a soma, teremos que colocar o termo genérico no formato
E isso já aprendemos no post anterior "Progressão Aritmética de ordem Superior".
Aprendemos também que a derivada N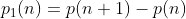 de
de 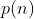 é:
é:
Aprendemos também que a derivada N
Assim, por indução inversa, concluímos que
Logo,
Assim, 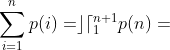
Exemplo. Suponha que 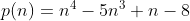 . Pelo triângulo das variações ( ver post anterior ) achamos rapidamente os coeficientes
. Pelo triângulo das variações ( ver post anterior ) achamos rapidamente os coeficientes 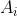 . Se o grau da função polinomial é
. Se o grau da função polinomial é 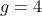 calculamos os
calculamos os 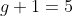 primeiros termos desta função:
primeiros termos desta função:
-11 -30 -59 -68 -3
-19 -29 -9 65
-10 20 74
30 54
24
Pegamos, então, os coeficientes 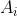 na diagonal da esquerda:
na diagonal da esquerda:
 ,
, 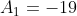 ,
, 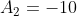 ,
,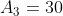 e
e 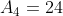
Portanto,
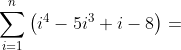

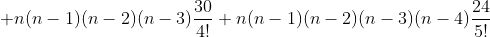
Ou, se preferirem, usando a notação de combinação , temos
Em um futuro post, mostrarei como achar a soma dos  primeiros termos de
primeiros termos de 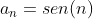 usando a integral N. / N.E: Veja esta matéria em Somatórios Trigonométricos
usando a integral N. / N.E: Veja esta matéria em Somatórios Trigonométricos




Interessante este post. Ao invés do gama maiúsculo, eu uso delta maiúsculo elevado a menos um.
ResponderExcluirNo papel eu utilizo um sinal de integral reticulado ( horizontal-vertical-horizontal, com as horizontais curtas e vertical alongada ).
ExcluirEu também.
ResponderExcluirExcelente Post.
Você já ouviu falar em Time Scales (escalas temporais)? É uma teoria recente que unifica o calculo contínuo e o discreto. A teoria tem uns 20 ou 30 anos.
É bastante interessante e até que simples (relativamente simples, tem coisa mais difícil), além de estar dando artigos interessantes (li alguns).
Obrigado pelo post, sempre adorei esse assunto.
Oi, Hugo, nunca ouvi falar. Tem alguns links?
ResponderExcluirNa parte de notas e referências do wikipedia tem alguns artigos.
ResponderExcluirhttp://en.wikipedia.org/wiki/Time_scale_calculus
Um site sobre o assunto
http://www.timescales.org/
Esse artigo é bem legal:
http://web.mst.edu/~bohner/papers/deotsas.pdf
E um livro, que fala sobre hiperreais também, é legal (não terminei de ler ainda):
http://mds.marshall.edu/etd/36/
Em portugues temos:
http://prope.unesp.br/xxii_cic/ver_resumo.php?area=100046&subarea=13058&congresso=30&CPF=38179586847
http://www.sbmac.org.br/eventos/cnmac/xxxiii_cnmac/pdf/563.pdf
Até +.
Obrigado.
Excluir