O valor de um terreno, cujo 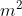 custa R$
custa R$ 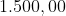 , pode ser calculado se conhecermos sua área, ou seja, quantos unidades de
, pode ser calculado se conhecermos sua área, ou seja, quantos unidades de 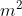 "cabem" dentro do mesmo. Se o terreno tiver um formato triangular com medidas conforme o diagrama abaixo
"cabem" dentro do mesmo. Se o terreno tiver um formato triangular com medidas conforme o diagrama abaixo
a tarefa fica fácil pois conhecemos a base
A área
Assim, 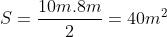 .
.
Então se o
Mas suponha que o leitor tenha um outro terreno triangular com as seguintes medidas
Conforme o modelo, sabemos o valor dos três lados do triângulo mas não de sua altura. E agora, como proceder para o cálculo da área deste terreno?
Em caso prático, o mais simples, talvez, seria esquecer as medidas dos lados 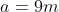 e
e 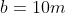 , pegar uma fita métrica e medir a desconhecida altura.
, pegar uma fita métrica e medir a desconhecida altura.
Porém, pode ocorrer do leitor ter apenas as medidas  ,
, e
e  anotadas e estar distante do terreno, resolvendo o negócio em outra localidade. Como calcular a área com esses dados?
anotadas e estar distante do terreno, resolvendo o negócio em outra localidade. Como calcular a área com esses dados?
Felizmente, podemos contar com o apoio póstumo do grande matemático, físico, engenheiro, inventor e astrônomo grego Arquimedes de Siracusa,
No entanto, a mais antiga demonstração que se conhece deste método se deve ao geômetra e também grego Heron de Alexandria,
O que nos foi legado por estes dois sábios da antiguidade, relativo ao cálculo da área de um triângulo a partir dos lados, é descrito a seguir.
Obs: nos cálculos, usarei aproximação de três casas decimais.
Primeiro soma-se os lados e divide-se por dois:
Aqui, o resultado  é conhecido como semiperímetro.
é conhecido como semiperímetro.
Em segundo, anota-se os resultados da diferença de  por cada lado:
por cada lado:
Em terceiro, multiplica-se  por cada diferença:
por cada diferença:
E em quarto e último, extra-se a raiz quadrado deste resultado:
Logo, a área do segundo triângulo é 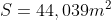 .
.
 O aprendiz pode treinar desenhando em um papel ( usando lápis ou caneta e uma
régua ) um triângulo qualquer e depois medir seus lados e altura
em
O aprendiz pode treinar desenhando em um papel ( usando lápis ou caneta e uma
régua ) um triângulo qualquer e depois medir seus lados e altura
em  . A tarefa fim é calcular ( usando ou não calculadora, como preferir ) a área com as fórmulas
. A tarefa fim é calcular ( usando ou não calculadora, como preferir ) a área com as fórmulas
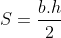
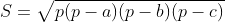
e comparar os valores encontrados.
e comparar os valores encontrados.
Aqui, o estudante prático pode dar-se por satisfeito pois já conhece estas duas ferramentas para o cálculo da área de um triângulo que pode usar para fins diversos: áreas de terrenos, provas / concursos, etc.
Mas para o estudante que, além de prático, é curioso e investigador ( e por isso leva uma grande vantagem sobre os demais ), que gosta saber a essência dos conhecimentos matemáticos, deve estar se perguntando porque a fórmula de Heron funciona, se não é que já sabe. Para estes entusiastas, segue a demonstração da fórmula de Heron, para conhecimento e/ou revisão.
Se ,
,  e
e  são os lados de um triângulo qualquer, então a área do mesmo é
são os lados de um triângulo qualquer, então a área do mesmo é
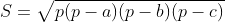 , com
, com 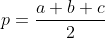
FÓRMULA DE HERON
Se
DEMONSTRAÇÃO
A demonstração será em duas partes ( 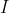 e
e 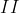 ).
).
Parte 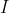
Considere o triângulo agudo - primeiro triângulo ( com ângulo 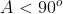 ) e o triângulo obtuso - segundo triângulo ( com ângulo
) e o triângulo obtuso - segundo triângulo ( com ângulo 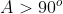 ), conforme os diagramas a seguir.
), conforme os diagramas a seguir.
Em ambos:
-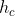 é a altura relativo ao lado
é a altura relativo ao lado  ;
;
- é a projeção do lado
é a projeção do lado  sobre a reta que contêm o lado
sobre a reta que contêm o lado  (
(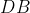 ). Reparem que se
). Reparem que se 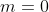 , podemos ter
, podemos ter 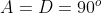 . Logo, estamos considerando também, embora implicitamente, o triângulo retângulo.
. Logo, estamos considerando também, embora implicitamente, o triângulo retângulo.
Nesta primeira etapa da demonstração, vamos provar que no primeiro triângulo vale a relação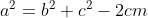 e, no segundo triângulo, vale
e, no segundo triângulo, vale 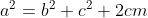 . Estas relações são as generalizações algébricas do teorema de pitágoras (
. Estas relações são as generalizações algébricas do teorema de pitágoras ( ), válidas para qualquer triângulo ( a generalização trigonométrica do
), válidas para qualquer triângulo ( a generalização trigonométrica do 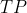 é chamada de Lei dos Cossenos ).
é chamada de Lei dos Cossenos ).
Usaremos o sinal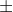 e diremos que a relação
e diremos que a relação 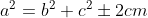 vale para ambos os triângulos. A idéia é provar os dois casos de um único modo.
vale para ambos os triângulos. A idéia é provar os dois casos de um único modo.
Sem mais delongas, observem que no triângulo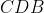 , tanto no primeiro quanto no segundo triângulo, de acordo com o
, tanto no primeiro quanto no segundo triângulo, de acordo com o 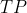 , temos
, temos
-
-
Nesta primeira etapa da demonstração, vamos provar que no primeiro triângulo vale a relação
Usaremos o sinal
Sem mais delongas, observem que no triângulo
Substituindo ( 2 ) em ( 1 ), obtemos
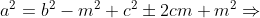
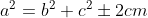
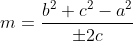
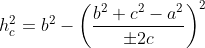
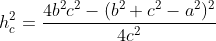
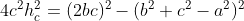
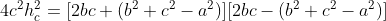
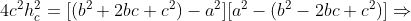
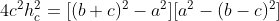
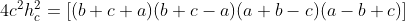
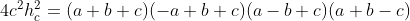 ( 3 )
( 3 )
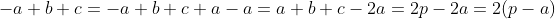
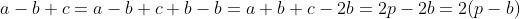
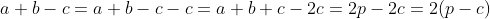
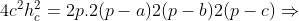
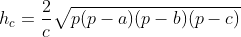
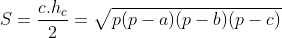
-*-
e está provado a relação conhecida como Lei das Projeções para um triângulo qualquer.
Parte 
Nesta segunda parte da demonstração, iremos calcular a altura 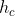 . Este é o segredo da fórmula de Heron: o cálculo da altura está embutido em função dos lados!
. Este é o segredo da fórmula de Heron: o cálculo da altura está embutido em função dos lados!
Da Lei das Projeções , tiramos:
Substituindo em ( 2 ):
Observem que, no segundo membro o 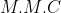 dos denominadores é
dos denominadores é 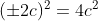 . Colocando o segundo membro em um denominador comum utilizando este
. Colocando o segundo membro em um denominador comum utilizando este 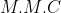 , temos
, temos
Multiplicando ambos os membros por 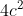 :
:
No segundo membro, usando o produto notável 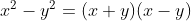 :
:
Reorganizando algebricamente cada fator entre colchetes, de forma que se forme os quadrados perfeitos 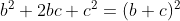 e
e 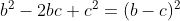 , temos
, temos
Agora em cada fator, utilizamos novamente o produto notável 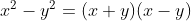
Vamos analisar estes fatores, principalmente os três últimos:
Sendo 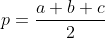 o semiperímetro ou
o semiperímetro ou 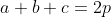 , temos
, temos
Substituindo esses resultados em ( 3 ):
E temos a altura do triângulo  relativa ao lado
relativa ao lado  . Agora basta usar o lado
. Agora basta usar o lado  como base e usarmos a fómula comum para o cálculo da área de um triângulo:
como base e usarmos a fómula comum para o cálculo da área de um triângulo:
Como podem perceber, essas engenhosas manipulações algébricas, vistas na demonstração, só podem ter saído da mente do grande Arquimedes.
-*-
PARA SABER MAIS:
No blog FATOS MATEMÁTICOS, do Prof. Paulo Sérgio, temos a demonstração da fórmula de Heron usando a Lei dos Cossenos.
No blog O BARICENTRO DA MENTE, de Kleber Kilhan, sugiro o post O Teorema de Steward, para quem desejar se aprofundar na geometria dos triângulos e saber um pouco sobre a vida deste matemático.
REFERÊNCIA BIBLIOGRÁFICA
Imagens: http://pt.wikipedia.org/wiki/Arquimedes
http://pt.wikipedia.org/wiki/Heron_de_Alexandria








Muito bom!
ResponderExcluirA propósito, outro livro sensacional sobre geometria é "CQD" de Gilberto Garbi. Caso não tenha visto, recomendo.
Abs (Cesar)
Obrigado pela dica, Cesar Rosa!
ResponderExcluirOi! Quando vi a fórmula de Heron achei interessante porque nela se extraia a raiz quadrada de metro elevado à quarta para dar metro quadrado e a decorei. Certa vez eu trabalhando no atendimento de um banco fui chamado ao setor de empréstimos, Tavano! me disse o chefe do setor, Temos um terreno dado em garantia e precisamos saber o valor dele para hoje, sabemos o preço do metro quadrado na região mas na escritura não consta a área e o terreno é triangular só consta a medida dos lados (talvez o escrivão não soubesse calcular) Nem é preciso dizer que Heron me salvou. Verifiquei depois que o triângulo não era retângulo o que deve ter dificultado o cálculo da área. Há certas informações que pensamos que jamais serão úteis. Obrigado
ResponderExcluirOi, Tavano
ExcluirA geometria plana talvez seja a parte da matemática com mais aplicações práticas porque partiu da necessidade do homem de demarcar suas terras. Isto, desde o começo das civilizações. De lá para cá, não se mudou muita coisa em relação as fórmulas. O que não se pode dizer o mesmo dos aparelhos de medições.
Na sua experiência relatada, vc tinha um ás na manga ( fórmula de Heron ) que fez com que aumentasse o conceito positivo com seu chefe.
Sobre informações que pensamos que jamais serão úteis, temos o caso moderno da geometria não-euclidiana que foi uma ferramenta indispensável para Einstein desenvolver sua Teoria da Relatividade.
Valeu, Tavano e obrigado pelo seu relato.
Novamente publicou um post com muita riqueza de detalhes. Vejo que também gosta de geometria. Com certeza este post será muito útil para todos que precisam saber mais sobre a fórmula de Heron. Obrigado pelo link citado acima.
ResponderExcluirDica: Acho que você devia criar uma página secundária com a lista de posts já publicados.
Oi, Prof. Paulo Sérgio,
ExcluirO treinamento que sugeri neste post eu fazia muito quando tinha uns 12 anos. Também bolei um jogo matemático de dupla onde ganhava quem desenhasse um triângulo cuja área se aproximasse o máximo de [;50cm^2;] sem ultrapassar este valor.
Ainda estou para aprender como coloco um menu embaixo do título do blog. O Kleber e o Valdir me passaram uns links que ainda não tive oportunidade para ler.
Obrigado pela dica, com certeza ela é útil.
Valeu.
Muito bom Aloísio. Gostei de ler e deixar melevar pelo seu raciocínio. Demorei um pouco para ler, pois infelizmente o tempo é curto para dar conta de tantos artigos excelentes e para um texto técnico, não dá para ler sem ter o mínimo de concentração.
ResponderExcluirObrigado por citar meu blog. No link abaixo tem o método de Heron para aproximações de raízes quadradas:
http://obaricentrodamente.blogspot.com/2008/11/mtodo-de-hero-para-aproximao-de-raz.html
Aproveitando, adicionei seu banner em minha lista de parceiros.
Abraços.
Oi, Kleber!
ResponderExcluirObrigado pelo elogio e força!
Olha, posso dizer que depois que li seu trabalho sobre o teorema de Steward me senti uma "autoridade" sobre triângulos. Não estou exagerando.
Eu olhei no seu link sobre o método de Heron para aproximar raízes e confesso que é outra novidade interessante para mim. Valeu!
Agradeço pelo banner e pela divulgação no seu prestigiado e tradicional blog.
Um grande abraço!
muito bem explicado, agora sim entendi vlw cara vc é o cara
ResponderExcluir