Os polígonos regulares com número de lados 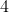 ,
,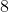 ,
,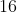 ,...,
,...,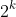 ( com
( com 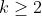 ), inscritos em um círculo de raio
), inscritos em um círculo de raio 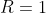 , estão relacionados de uma forma especial, com curiosa referência à raíz quadrada de
, estão relacionados de uma forma especial, com curiosa referência à raíz quadrada de  .
.
De fato, sendo 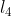 ,
, 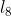 ,
, 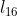 ,...,
,...,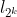 as medidas destes lados, temos que
as medidas destes lados, temos que
de forma que a quantidade de  sob radicais é sempre
sob radicais é sempre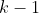 .
.
A demonstração deste fato é simples, conforme se verifica com uma leitura atenta e análise da figura a seguir. Bastam conhecimentos sobre área de triângulo, teorema de pitágoras e equação do 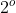 grau.
grau.

Seja o segmento 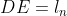 a medida do lado de um polígono de
a medida do lado de um polígono de  lados inscrito em um círculo de raio
lados inscrito em um círculo de raio 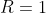 (
(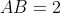 ). Logo,
). Logo, 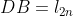 é a medida do lado de um polígono inscrito de
é a medida do lado de um polígono inscrito de 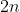 lados;
lados;
Qualquer triângulo inscrito em um semi-círculo é retângulo. Logo, podemos calcular a área  do triângulo
do triângulo 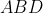 de duas formas:
de duas formas:
Substituindo nestas expressões 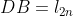 ,
, 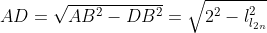 ,
, 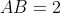 e
e 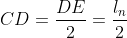 , temos
, temos
O próximo passo é colocar 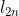 em função de
em função de 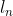 . Para facilitar, faremos
. Para facilitar, faremos 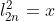 e
e 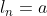 . Assim,
. Assim,
E para pegarmos a raiz que interessa, vejam que o menor número de lados do tipo 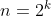 para um polígono inscrito é
para um polígono inscrito é 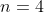 ( quadrado ). Pelo teorema de pitágoras, calculamos facilmente
( quadrado ). Pelo teorema de pitágoras, calculamos facilmente  , ou
, ou 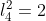 . Portanto, como
. Portanto, como 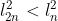 , concluimos que l^2_{2n} < 2. Logo, da última expressão só nos resta
, concluimos que l^2_{2n} < 2. Logo, da última expressão só nos resta
Com esta fórmula recursiva, que relaciona o polígono de 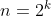 lados com o polígono de
lados com o polígono de 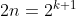 lados, ambos inscritos em um círculo de raio
lados, ambos inscritos em um círculo de raio 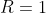 (
( 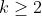 , ou seja,
, ou seja, 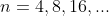 , etc ), veremos como podemos obter as expressões para a medida do lado do polígono
, etc ), veremos como podemos obter as expressões para a medida do lado do polígono 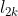 , mostradas no início do artigo.
, mostradas no início do artigo.
De  para
para 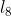
De 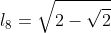 para
para 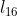
De 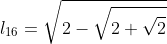 para
para 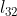
E assim, por diante, de forma que
Observação: Como um polígono regular com um grande número de lados inscrito em um círculo se assemelha ao mesmo, é fácil perceber que
tendo em vista que 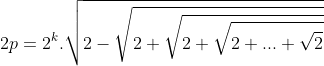 é o perímetro do polígomo regular inscrito e
é o perímetro do polígomo regular inscrito e 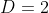 é o diâmetro do círculo unitário.
é o diâmetro do círculo unitário.
Referência bibliográfica:
O que é a Matemática?, de Richard Courant e Herbert Robbins, Editora Ciência Moderna, 2000.

Oi, Teixeira! Esse problema (ou parecido) caiu num vestibular da Poli-Usp lá pelos anos ¨60. Segundo a lenda urbana houve 60% de notas "zero". Um outro problema desse mesmo vestibular era provar que uma certa equação cúbica só tinha uma raiz real, a solução era "fácil" era "só" provar que a derivada não se anulava, mas vai lembrar!!CURIOSIDADE: Você conhece algum método que para todo p=4k+1 forneça a e b tal que a^2+b^2=p? já vi várias vezes essa pergunta em fóruns mas nunca foi resolvida. abçs
ResponderExcluirOi, amigo Tavano! Que saudades!
ResponderExcluirEsta é uma questão clássiquerríma da geometria das mais interessantes.
Lenda urbana, é, rs.Pelo índice de reprovação, acredito que o problema não foi direto.
Tão simples a questão da cúbica, não? As vezes pensamos só na álgebra, mas em uma questão como essa, se pensarmos no formato do gráfico da função cúbica correspondente, perceberemos que equações do tipo y=a(x+b)^3+c só tem uma raíz porque a derivada não se anula. Na verdade, esta equação é apenas uma translação horizontal e vertical de y=ax^3.
Tavano, acho que vi algo sobre a^2+b^2=4k+1 em um livro que tenho. Depois retorno.
Outro abraço!
Olá,Aloísio!
ResponderExcluirEste post é realmente magnífico.Esta fórmula de recorrência é muito bela e útil,e foi muito bem colocado por você quando escreveu sobre este tipo de análise ser clássica.
No entanto,oque mais me chamou a atenção foi a identidade de π.
Como posso mostrar esta identidade sem partir de algo tão intuitivo como prever que "um polígono regular com um grande número de lados inscrito em um círculo se assemelha ao mesmo". Ou em outras palavras, partir apenas da equação à direita da igualdade e dela mostrar que tal limite é π?
Grande abraço!
Oi, Diogo!
ResponderExcluirObrigado, que bom que gostou.
Na verdade eu queria dizer que essa teoria era classiquérrima e não clássiquerríma, kkk
A demonstração da fórmula para o pi é teórica e tão certa quanto pi=circunferência/diâmetro.
O que podemos fazer é, através da fórmula, e já que não podemos operar infinitas raízes de 2, é calcular as aproximações do pi, para l4, l8, l16, etc.
Eu usando uma planilha eletrônica, tipo EXCEL, verifiquei estas aproximações cada vez melhores para o pi.
Outro abraço, diogo!!
Olá, Aloísio!!!!
ResponderExcluirGrande Aloísio, parabéns!!!! Depois dessas explicações e também, da demonstração para obter-se a fórmula para... L2k, aquela lenda urbana que o Tavano citou ali acima, não será reeditada!!!! Já pensou, 60% de notas zeros em um vestibular superconcorrido???? Um trem de transporte de minérios da Vale, seguramente possui menos rodas do que isso!!! KKKKKKKK!!!!!!
O interessante desse estudo, é que... não é preciso necessariamente de um conhecimento superior em matemática, como você afirmou no início do post, para se fazer a demonstração disso. Formidável!!!!
Um abraço!!!!!
Oi, Valdir!
ResponderExcluirObrigado! Tendo em vista estas representações dos lados com raízes quadradas de 2, todos os polígonos com números de lados 2^k são construtíveis com régua e compasso.
As vezes empregamos arsenal pesado onde uma técnica mais leve resolve como é o segundo método ( do Cézer ) para calcular o ponto máximo de (y^2+x)^2=x
Abraços