Definição
De todas as equações algébricas(polinomiais) de enésimo grau, a mais simples é
conhecida como Equação Ciclotômica, exaustivamente estudada por Euler e Gauss.
Mas conforme o Teorema Fundamental da Álgebra ( -ver post 022), esta equação possui
-ver post 022), esta equação possui  raízes complexas e os gráficos acima não fornecem um mínimo de pista sobre onde se encontram as outras.
raízes complexas e os gráficos acima não fornecem um mínimo de pista sobre onde se encontram as outras.
Para calcular as raízes complexas reais mostradas, é necessário apenas isolar a variável no primeiro membro para obtermos as raízes enésimas da unidade.
Assim, da equivalência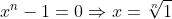 e pelo
e pelo  , fica claro que
, fica claro que
Mas conforme o Teorema Fundamental da Álgebra (
Para calcular as raízes complexas reais mostradas, é necessário apenas isolar a variável no primeiro membro para obtermos as raízes enésimas da unidade.
Assim, da equivalência
A) Se  for ímpar, então
for ímpar, então 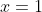 , o que indica que temos ainda um número par de
, o que indica que temos ainda um número par de 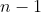 raízes complexas;
raízes complexas;
B) Se  for par, então
for par, então 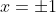 .o que indica que temos ainda um número também par de
.o que indica que temos ainda um número também par de 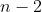 raízes complexas.
raízes complexas.
Como calcular estas outras raízes complexas? Para isto, veremos um breve resumo específico sobre números complexos.
Um número complexo é todo número da forma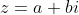 , com
, com  e
e  reais e
reais e 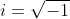 é a unidade imaginária. A característica principal de
é a unidade imaginária. A característica principal de  é que
é que 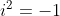 , uma igualdade que nenhum número real pode estabelecer.
, uma igualdade que nenhum número real pode estabelecer.
Como calcular estas outras raízes complexas? Para isto, veremos um breve resumo específico sobre números complexos.
Os Números Complexos
Um número complexo é todo número da forma
O módulo do número complexo
Os números complexos são representados no plano de Argand-Gaus. Consiste em dois eixos ortogonais orientados onde o eixo horizontal contêm a parte real de
Assim, o ponto  representa o número complexo
representa o número complexo 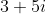 enquanto o ponto
enquanto o ponto  representa o número complexo
representa o número complexo 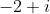 .
.
O ponto 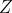 designa genericamente qualquer número complexo
designa genericamente qualquer número complexo 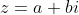 .
.
Observem agora o que significa o módulo de  . Nada mais é do que a distância da origem ao ponto que o representa, ou seja,
. Nada mais é do que a distância da origem ao ponto que o representa, ou seja, 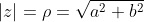 , um número real sempre positivo.
, um número real sempre positivo.
Importante observar que qualquer número real também é um número complexo. O número 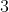 , por exemplo, representado pelo ponto
, por exemplo, representado pelo ponto 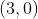 é o número complexo
é o número complexo 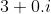 .
.
O ângulo  é chamado de argumento de
é chamado de argumento de  . Com ele podemos representar o número complexo
. Com ele podemos representar o número complexo  na sua forma trigonométrica ou polar, conforme a seguir.
na sua forma trigonométrica ou polar, conforme a seguir.
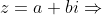
De 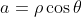 e
e 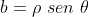 vem,
vem,
Na forma polar, a multiplicação entre dois números complexos fica bastante facilitada. De fato pois,
Então, para multiplicar dois números complexos na forma trigonométrica, basta multiplicar os módulos e somar os argumentos.
Demonstração. Temos que ter em mente o seguinte.
E ainda,
Agora é só usar (1) para multiplicar os números complexos
Obtendo
E aplicando (2) e (3), chegamos ao produto polar
_*_
Logo, se multiplicármos  números complexos iguais, ou seja, de mesmos módulos e argumentos, temos
números complexos iguais, ou seja, de mesmos módulos e argumentos, temos
que é a expressão polar para a potência enésima de um número complexo conhecida como fórmula de Moivre.
_*_
De modo inverso, podemos dizer que a raíz enésima de um número complexo é também um número complexo. Assim,
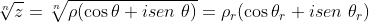
onde 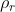 e
e 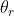 são o módulo e o argumento da raíz enésima de
são o módulo e o argumento da raíz enésima de  , respectivamente.
, respectivamente.
Elevando à potência , temos
, temos
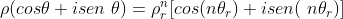
Portanto, da identidade de números complexos, os módulos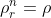 e os argumentos
e os argumentos 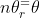 são iguais ou equivalentes. Logo, o módulo da raíz enésima de
são iguais ou equivalentes. Logo, o módulo da raíz enésima de  é
é 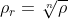 . Levando em conta que estamos tratando com funções trigonométricas periódicas, o argumento
. Levando em conta que estamos tratando com funções trigonométricas periódicas, o argumento 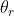 da raíz enésima de
da raíz enésima de  calcula-se da seguinte maneira:
calcula-se da seguinte maneira:
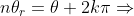
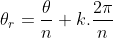
Elevando à potência
Portanto, da identidade de números complexos, os módulos
Aqui nos parece que temos infinitos argumentos 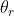 de infinitas raízes enésimas de
de infinitas raízes enésimas de  , pois pelo que estudamos em trigonometria, sabemos que
, pois pelo que estudamos em trigonometria, sabemos que 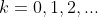 .No entanto, serão necessários utilizar apenas alguns valores de
.No entanto, serão necessários utilizar apenas alguns valores de  . Precisamente, são utilizados
. Precisamente, são utilizados  valores de
valores de  , justificando assim, a existência de
, justificando assim, a existência de  raízes enésimas do número complexo
raízes enésimas do número complexo  (conforme o
(conforme o  ).
).
Como podemos entender isto? Considere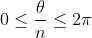 e
e 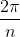 o ângulo central de uma das fatias de uma circunferência dividido em
o ângulo central de uma das fatias de uma circunferência dividido em  partes. Assim, da posição angular
partes. Assim, da posição angular  , vamos acrescentando fatias iguais de ângulo central de
, vamos acrescentando fatias iguais de ângulo central de 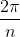 , ou seja ,
, ou seja ,

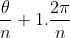

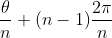
Como podemos entender isto? Considere
...................
Ora, mas nesta última expressão 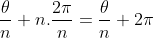 e os valores trigonométricos
e os valores trigonométricos  e
e 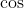 são equivalentes à
são equivalentes à  e voltamos a posição inicial. Portanto, os valores diferentes das
e voltamos a posição inicial. Portanto, os valores diferentes das  raízes enésimas de
raízes enésimas de  ocorrem quando
ocorrem quando 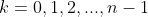 . Resumindo, para estas condições de
. Resumindo, para estas condições de  :
:
Resolução da Equação Ciclotômica
Com 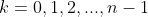
Exemplo 1 (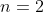 )
)
Neste caso, seria desnecessário usar a fórmula polar se o objetivo não fosse verificar o seu funcionamento. Porque, pelo  , só temos aqui duas raízes complexas e elas são os números reais
, só temos aqui duas raízes complexas e elas são os números reais 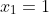 e
e 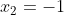 . Mas vejamos o que acontece se inserirmos o grau da equação
. Mas vejamos o que acontece se inserirmos o grau da equação 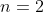 na expressão:
na expressão:
Com 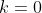 ou
ou 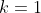
Para 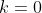 , temos
, temos 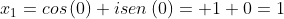
Para 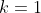 , temos
, temos 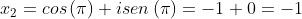
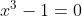
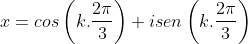
Com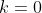 ,
, 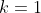 ou
ou 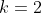
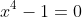
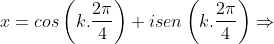
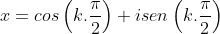
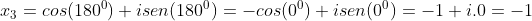
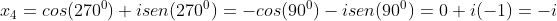
No plano de Argand-Gauss, os segmentos que representam os módulos das raízes enésimas da unidade, formam entre si, ângulos de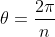 , de forma que os pontos que representam estas raízes formam um polígono regular de
, de forma que os pontos que representam estas raízes formam um polígono regular de  lados. Por este motivo, a equação
lados. Por este motivo, a equação 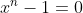 recebe o nome de Equação Ciclotômica. Gauss utilizou esta curiosa propriedade e, após analisar a permutação das raízes, descobriu, de forma magnânima, que o polígono de
recebe o nome de Equação Ciclotômica. Gauss utilizou esta curiosa propriedade e, após analisar a permutação das raízes, descobriu, de forma magnânima, que o polígono de 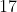 lados é construtível com régua e compasso.
lados é construtível com régua e compasso.
Exemplo 2 (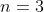 )
)
Com
Lembrando que 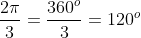 ,
,
para 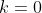 , temos
, temos 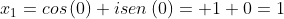
para 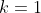 , temos
, temos 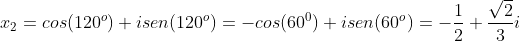
para 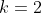 , temos
, temos 
Exemplo 3 (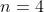 )
)
Com 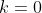 ,
, 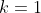 ,
, 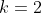 e
e 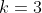
Lembrando que 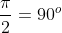 ,
,
Para 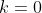 , temos
, temos 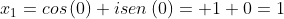
Para 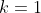 , temos
, temos 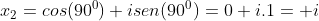
Para 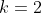 , temos
, temos
Para 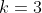 , temos
, temos
Representação no Plano Complexo
No plano de Argand-Gauss, os segmentos que representam os módulos das raízes enésimas da unidade, formam entre si, ângulos de
Referência Bibliográfica
- Fundamentos de Matemática Elementar, Vol. 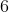 - Complexos, Polinômios, Equações - Atual Editora
- Complexos, Polinômios, Equações - Atual Editora
-O Romance das Equações Algébricas, de Gilberto G.Garbi, Editora Makron Books, 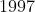 .
.
Gostará de ler também:
008-Logaritmo de Número Negativo?
022-O Teorema Fundamental da Álgebra
078-As Fórmulas de Bháscara e Cardano pelas Relações de Girard





Mais um artigo valioso para nós, leitores.
ResponderExcluirOs números complexos realmente possuem propriedades bem intrigantes.
Penso no quanto Moivre poderia contribuir para a matemática, se acertadamente escolhesse exercer esta profissão.
Abraços, Aloísio.
Oi, Diogo.
ResponderExcluirLi, em pesquisa, que o francês Abraham de Moivre (1667-1754) foi membro da Royal Society e grande amigo de Isaac Newton e Edmond Haley. Temos aquele ditado: dize-me com quem andas que direi quem tu és. De fato, era um gênio.
Era matemático, mas acho que ganhava a vida com seguros.
Valeu!
Muito obrigado por dedicar seu tempo a escrever esse excelente post!
ResponderExcluirDe nada, Darius!
ResponderExcluirSeja bem vindo e espero que tenha tido proveito com esta matéria.
Um abraço!