O objetivo do presente artigo é calcular os valores de
Já vimos, no artigo anterior, as seguintes representações de
Algébrica: 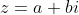
Geométrica: 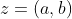
Trigonométrica: 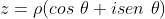
Forma Exponencial de um Número Complexo
Um modo de chegar na forma exponencial é pensar em  na forma trigonométrica como uma função de
na forma trigonométrica como uma função de  (em radianos), derivar e resolver a equação diferencial correspondente, ou seja
(em radianos), derivar e resolver a equação diferencial correspondente, ou seja
Mas em 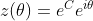 e
e  temos
temos 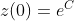 e
e 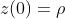 , respectivamente, de forma que
, respectivamente, de forma que 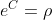 . Chegamos, então, a forma exponencial do número complexo
. Chegamos, então, a forma exponencial do número complexo 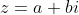 :
:
Onde 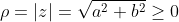 é o módulo de
é o módulo de  e
e  é o argumento de
é o argumento de  .
.
Agora, para achar uma expressão para 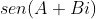 , façamos
, façamos 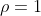 e calculamos
e calculamos
de forma que
Mas,
Substituindo estas equivalências na expressão final e efetuando a diferença do segundo membro, chegamos a conclusão que
ou
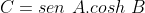
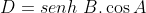
No caso de 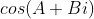 , usamos agora
, usamos agora
Fazendo 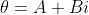 e
e 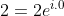 , desenvolvendo e separando a parte real e imaginária, chegamos analogamente à
, desenvolvendo e separando a parte real e imaginária, chegamos analogamente à
ou
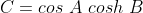
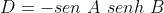
Para 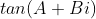 , basta fazer
, basta fazer
e usar a fórmula conhecida de divisão de dois números complexos na forma algébrica
Fica como exercício aos leitores.
Referência Bibliográfica
-História da Matemática, de Carl B.Boyer, Editora Edgard Blücher LTDA, 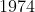 ;
;
- Fundamentos de Matemática Elementar, Vol.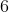 - Complexos, Polinômios, Equações - Atual Editora;
- Complexos, Polinômios, Equações - Atual Editora;
- Fundamentos de Matemática Elementar, Vol.
-O Romance das Equações Algébricas, de Gilberto G.Garbi, Editora Makron Books, 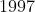 .
.
Gostará de ler também:


Olá, Aloisio!
ResponderExcluirEstá de parabéns pelo post! Muito bom mesmo!
Só tenho uma dúvida; Como você tem feito para escrever em LaTex no blogger?
Por acaso, meu script pro firefox tem dado errado, e gostaria de saber alternativas.
Abraços,
João Pedro.
Oi, João Pedro!
ExcluirObrigado!
Desde quando tive problemas com o latex no Firefox estou usando uma sugestão do Kleber. É um editor online de equações:
http://www.codecogs.com/latex/eqneditor.php
Valeu, nobre.
Nossa Aloisio, está de parabéns com este post, pois usou uma abordagem que eu não conhecia, ou seja, deduziu a relação de Euler sem usar séries infinitas. Como sugestão para ficar mais elegante o post, usa as funções seno e cosseno hiperbólico que são dadas por
ResponderExcluir[;\sinh B = \frac{e^B - e^{-B}}{2};]
e
[;\cosh B = \frac{e^B + e^{-B}}{2};]
Oi, Paulo!
ResponderExcluirObrigado pelos elogios e pela sugestão. Como não tenho muita intimidade com funções hiperbólicas, nem saquei à primeira vista. Mas já fiz os complementos.
Valeu!