Considere a elipse mostrada no gráfico cartesiano do diagrama. Observem que a mesma tem centro na origem 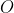 , raio maior
, raio maior 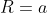 paralelo ao eixo
paralelo ao eixo 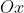 e raio menor
e raio menor 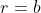 paralelo ao eixo
paralelo ao eixo 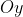 . Nestas condições, a equação da elipse é
. Nestas condições, a equação da elipse é 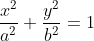 . Na forma explícita
. Na forma explícita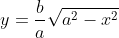 , pode ser considerada a lei de definição de uma função cujo gráfico encontra-se no mesmo diagrama, acima do eixo
, pode ser considerada a lei de definição de uma função cujo gráfico encontra-se no mesmo diagrama, acima do eixo 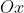 .
.
Com o objetivo de calcular a área  da elipse usando Cálculo, integraremos a função considerada
da elipse usando Cálculo, integraremos a função considerada 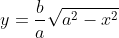 no intervalo
no intervalo 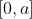 , multiplicando o resultado por
, multiplicando o resultado por 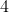 , ou seja
, ou seja
Fazendo,
com as seguintes alterações nos limites inferior e superior da integral:
temos,
Mas, 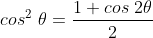 e, substituindo, vem
e, substituindo, vem
Assim, o valor desta integral definida é
Para calcular a área da elipse com uma integral utilizando a variável  e os limites
e os limites  e
e  , basta reverter a transformação trigonométrica
, basta reverter a transformação trigonométrica 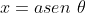 em
em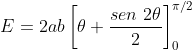 , nos mesmos moldes do artigo 086 .
, nos mesmos moldes do artigo 086 .
Se 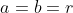 , temos um círculo e, portanto,
, temos um círculo e, portanto, 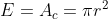 .
.
Gostará de ler também:


por que multiplica por 4?
ResponderExcluirJá que todas as "fatias" da elipse são iguais, com esses limites de integração ele só está calculando a área da "fatia" da elipse que se encontra no primeiro quadrante. Multiplicando o resultado por 4, tem-se então a área de toda a elipse.
ExcluirPorque x=a sen(Teta) , E não x= a cos(Teta)?
ResponderExcluirIntegral trigonométrica
ResponderExcluirIntegral trigonométrica
ResponderExcluirQual livro tem essa demonstracao
ResponderExcluirA área do círculo é A = (pi)xR² porque os "raios" são iguais. Já na elipse, os raios são diferentes: R1 # R2. Então a área da elipse fica assim: A = (pi)*R1*R2.
ResponderExcluirEsta demonstração está incorreta.