Ref: [ 088-Equações Recíprocas ( Parte 1/3) ]
[ 089-Equações Recíprocas ( Parte 2/3 )]
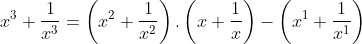
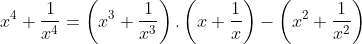
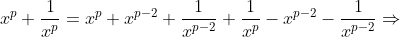
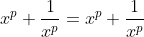
Este é o modo de mudança de variável que faremos nas equações recíprocas na forma normal. Veremos, agora, que efeito esta substituição causará nas identidades para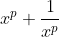
, quando utilizadas de forma recursiva. Vamos precisar apenas dos expoentes 
.
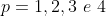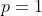
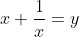
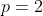
\left(x+\frac{1}{x}%20\right%20)-\left(x^0+\frac{1}{x^0}%20\right%20)\Rightarrow "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
(y)-2%20\Rightarrow "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
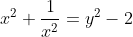
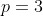
\left(x+\frac{1}{x}%20\right%20)-\left(x^1+\frac{1}{x^1}%20\right%20)\Rightarrow "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
y-(y)%20\Rightarrow "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
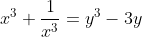
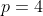
\left(x+\frac{1}{x}%20\right%20)-\left(x^2+\frac{1}{x^2}%20\right%20)\Rightarrow "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
(y)-(y^2-2)%20\Rightarrow "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
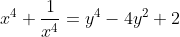
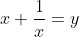
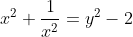
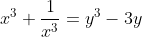
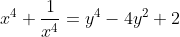
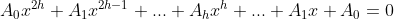
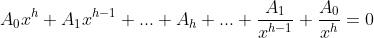
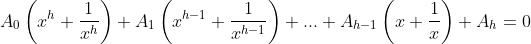
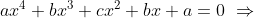
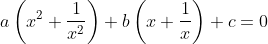
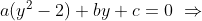
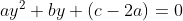
Introdução
Conforme a Teoria dos Grupos, cujo pioneiro foi o matemático francês Evarist Galois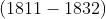 
, uma equação polinomial é resolúvel algebricamente, de modo geral, até o 
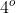grau, excetuando-se os casos particulares de graus superiores.
Como exemplo destas exceções, temos a equação quíntica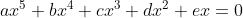
; a equação de enésimo grau pura 
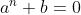; a equação 
-quadrática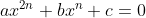 
; a equação geométrica 
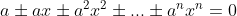, onde os sinais são todos iguais ou alternados; dentre outras; e as equações recíprocas.
Não considerando a série geométrica, as equações recíprocas, no quesito grau, foram as mais longes equações polinomiais completas resolúveis algebricamente. Uma equação recíproca qualquer é resolúvel até o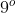
grau, enquanto uma equação recíproca de grau par e de segunda classe é resolúvel até o 
grau.
Já sabemos que qualquer equação recíproca de grau ímpar pode ter o grau reduzido em uma unidade e uma equação recíproca de grau par e de segunda classe pode ter o grau reduzido em duas unidades. O resultado destas reduções é sempre uma equação recíproca de grau par e de primeira classe chamada de forma normal. Logo, uma equação recíproca na forma normal é resolúvel algebricamente até o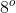
grau.
No presente artigo, tratarei das equações recíprocas de grau par e de primeira classe ou de forma normal e limitarei apenas a demonstrar a possibilidade de resolução das equações deste tipo, d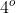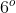e, 
e 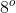graus, mesmo porque o formato das raízes das equações reciprocas de grau 
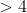são construções numéricas, envolvendo radicais, bastante complexas, sem finalidade prática.
Então, a essência deste post é justamente o dito artifício algébrico da redução à metade do grau. Vamos à ele.
Começaremos dizendo que a identidade a seguir é muito útil no trato com as equações recíprocas.
Dados o inteiro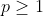 
e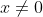 
, temos a seguinte identidade algébrica:
.
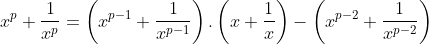
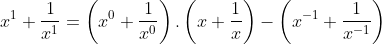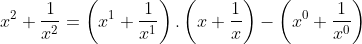
Como exemplo destas exceções, temos a equação quíntica
Não considerando a série geométrica, as equações recíprocas, no quesito grau, foram as mais longes equações polinomiais completas resolúveis algebricamente. Uma equação recíproca qualquer é resolúvel até o
Já sabemos que qualquer equação recíproca de grau ímpar pode ter o grau reduzido em uma unidade e uma equação recíproca de grau par e de segunda classe pode ter o grau reduzido em duas unidades. O resultado destas reduções é sempre uma equação recíproca de grau par e de primeira classe chamada de forma normal. Logo, uma equação recíproca na forma normal é resolúvel algebricamente até o
No presente artigo, tratarei das equações recíprocas de grau par e de primeira classe ou de forma normal e limitarei apenas a demonstrar a possibilidade de resolução das equações deste tipo, de
A teoria geral é esta: as equações recíprocas na forma normal de grau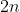 
, por intermédio de um artifício algébrico, tem seu grau reduzido à uma equação polinomial de natureza diversa, de grau . Assim temos as reduções de grau de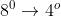 
( resolúvel pela fórmula de Ferrari ), de 
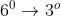( resolúvel pela fórmula de Cardano-Tartaglia ) e de 
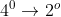( resolúvel pela fórmula de Bhaskara ).
Então, a essência deste post é justamente o dito artifício algébrico da redução à metade do grau. Vamos à ele.
Começaremos dizendo que a identidade a seguir é muito útil no trato com as equações recíprocas.
Identidade Algébrica para 
Exemplos
Demonstração. Muito simples. Apenas multiplique o segundo membro da identidade e elimine os termos iguais.
Observem que esta identidade é válida para qualque valor complexo de 
. Mas como estamos lidando com expoentes inteiros e positivos, fiz a restrição 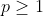, sendo um número natural.
A substituição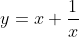 
Este é o modo de mudança de variável que faremos nas equações recíprocas na forma normal. Veremos, agora, que efeito esta substituição causará nas identidades para
RESUMO
Veremos a seguir, de que maneira estas substituições se encaixam na resolução das equações recíprocas. A partir daqui, estudaremos efetivamente as equações recíprocas de forma normal.
Resolução da Equação Recíproca de Grau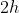 
, com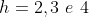 
e de Primeira Classe
Seja a equação
Sendo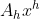 
o termo central. Dividindo ambos os membros por 
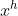, temos
Agrupando os termos de coeficientes iguais:
E aqui entra as substituições do RESUMO. Vejamos os casos particulares.
Resolução da Equação Recíproca de 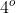Grau e de Primeira Classe
Fazendo 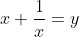, temos
O objetivo foi alcançado, ou seja, o grau da equação original foi reduzido pela metade e a equação em 
é resolúvel pela fórmula de Bháskara.
Para cada raiz calculada, encontramos um par de raízes 
por intermédio da equação de substituição 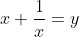ou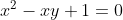 
que é uma equação quadrática comum em todas as equações recíprocas estudadas neste artigo.
Resolução da Equação Recíproca de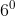 
Grau e de Primeira Classe
Fazendo
A equação cúbica em , após uma preparação, é resolúvel pela fórmula de Cardano-Tartaglia. Os valores de são encontrados pela equação quadrática 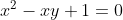. Desta forma, encontramos as seis raízes da equação original.
Resolução da Equação Recíproca de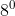 
Grau e de Primeira Classe
Fazendo
Que é resolúvel pelo método de Ferrari. Como nos dos casos anteriores, a equação quadrática 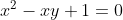fornece dois valores de para cada raiz encontrada. Desta forma, as oito raízes da equação original são calculadas.
_*_
Referência bibliográfica:
-Matemática, Terceiro Ano Colegial, Ary Quintella, Companhia Editora Nacional, São Paulo, 1968;
- Fundamentos de Matemática Elementar, Vol.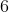 
- Complexos, Polinômios, Equações - Atual Editora;
-O Romance das Equações Algébricas, de Gilberto G.Garbi, Editora Makron Books,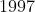 
.
Nenhum comentário:
Postar um comentário