Ref: [ 088-Equações Recíprocas ( Parte 1/3) ]
Forma Normal de uma Equação Recíproca
A equação recíproca de grau par e de primeira classe
a que se pode reduzir a resolução de todas as outras, chama-se forma normal de uma equação recíproca.
Portanto, são redutíveis à forma normal as seguintes equações recíprocas:
esgotando, assim, todas as possibilidades.
Redução à Forma Normal
Para reduzir uma equação 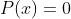 de primeira classe e de grau ímpar à forma normal, divide-se
de primeira classe e de grau ímpar à forma normal, divide-se 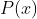 por
por 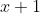 .
.
Demonstração. Neste caso, temos
Sendo esta equação de grau ímpar, a mesma tem uma quantidade par de termos. Os termos equidistantes dos extremos correspondem-se dois a dois. Por definição, em uma equação recíproca de primeira classe, estes termos correspondentes são iguais. Logo, 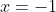 é raiz porque em
é raiz porque em 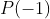 os termos de grau ímpar trocam de sinal e os de grau par conservam o sinal, ocorrendo o anulamento entre estes termos.
os termos de grau ímpar trocam de sinal e os de grau par conservam o sinal, ocorrendo o anulamento entre estes termos.
Segue que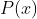 é divisível por
é divisível por 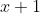 e o polinômio quociente
e o polinômio quociente 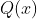 desta divisão, quando considerado como equação, conterá as raízes recíprocas restantes, conforme a seguir.
desta divisão, quando considerado como equação, conterá as raízes recíprocas restantes, conforme a seguir.
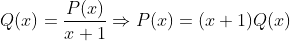
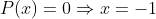 ou
ou 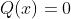
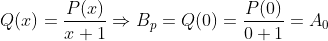
EXEMPLOS

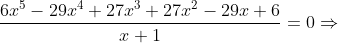
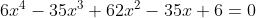
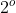 Caso: Equação de grau ímpar e de segunda classe
Caso: Equação de grau ímpar e de segunda classe
Para reduzir uma equação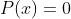 de segunda classe e de grau ímpar à forma normal, divide-se
de segunda classe e de grau ímpar à forma normal, divide-se 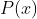 por
por 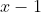 .
.
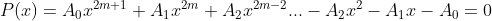
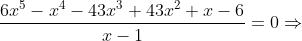
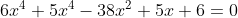
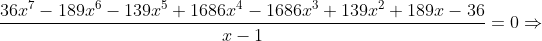
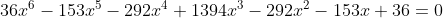
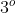 Caso: Equação de grau par e de segunda classe
Caso: Equação de grau par e de segunda classe
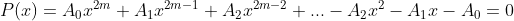
Conforme foi provado no artigo anterior, este tipo de equação é desprovido do termo central. Então, novamente, temos uma equação recíproca com uma quantidade par de termos. Como os termos equidistantes dos extremos são simétricos,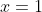 é uma raiz e
é uma raiz e 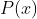 é divisível por
é divisível por 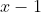 . Mas então, teríamos como quociente um polinômio
. Mas então, teríamos como quociente um polinômio 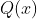 , de forma que
, de forma que 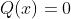 é uma equação recíproca de grau ímpar e de primeira classe. Então recaímos no
é uma equação recíproca de grau ímpar e de primeira classe. Então recaímos no 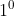 caso, no qual teremos que dividir
caso, no qual teremos que dividir 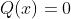 por
por 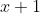 para obtermos, como resultado, uma equação
para obtermos, como resultado, uma equação 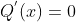 de grau par e de primeira classe e, portanto, da forma normal.
de grau par e de primeira classe e, portanto, da forma normal.
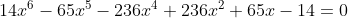
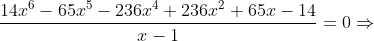
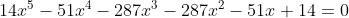
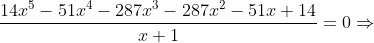
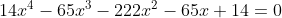
Segue que
Sabemos que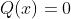 tem grau par e é recíproca. Como saberemos que esta equação é de primeira classe? Basta analisar o primeiro coeficiente
tem grau par e é recíproca. Como saberemos que esta equação é de primeira classe? Basta analisar o primeiro coeficiente 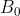 e o termo independente
e o termo independente 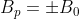 de
de 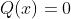 . No produto
. No produto 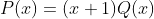 é fácil perceber que o coeficiente do termo de maior grau de
é fácil perceber que o coeficiente do termo de maior grau de 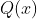 é igual ao coeficiente do termo de maior grau de
é igual ao coeficiente do termo de maior grau de 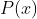 ou seja,
ou seja, 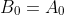 . Já o termo independente
. Já o termo independente 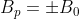 de
de 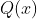 é
é 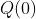 , veja:
, veja:
Logo, 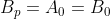 e concluímos que a equação de grau par
e concluímos que a equação de grau par 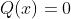 é de primeira classe e, portanto, encontra-se na forma normal.
é de primeira classe e, portanto, encontra-se na forma normal.
Para reduzir uma equação
Demonstração. Neste caso, temos
Aqui também temos uma quantidade par de termos. Mas desta vez, os termos equidistantes dos extremos são simétricos. É claro que 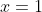 é uma raiz. Portanto, com um raciocínio similar a seção anterior, temos que
é uma raiz. Portanto, com um raciocínio similar a seção anterior, temos que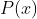 é divisível por
é divisível por 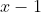 e o quociente
e o quociente 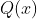 será de grau par contendo as raízes recíprocas restantes.
será de grau par contendo as raízes recíprocas restantes.
No produto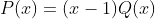 percebemos que o coeficiente do termo de maior grau de
percebemos que o coeficiente do termo de maior grau de 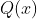 é igual ao coeficiente do termo de maior grau de
é igual ao coeficiente do termo de maior grau de 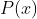 ou seja,
ou seja, 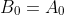 . Sendo que o termo independente
. Sendo que o termo independente de
de 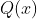 é
é 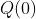 :
:
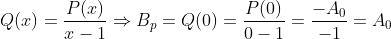
No produto
Logo, 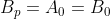 e concluímos que a equação de grau par
e concluímos que a equação de grau par 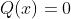 é de primeira classe e, portanto, encontra-se na forma normal.
é de primeira classe e, portanto, encontra-se na forma normal.
EXEMPLOS
Para reduzir uma equação 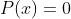 de segunda classe e de grau par à forma normal, divide-se
de segunda classe e de grau par à forma normal, divide-se 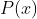 por
por 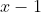 e por
e por 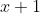 .
.
Demonstração. Neste caso, temos
Conforme foi provado no artigo anterior, este tipo de equação é desprovido do termo central. Então, novamente, temos uma equação recíproca com uma quantidade par de termos. Como os termos equidistantes dos extremos são simétricos,
EXEMPLO
Vamos reduzir à forma normal a equação recíproca de grau par e de segunda classe
Dividindo por 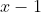 , temos
, temos
ou seja, uma equação recíproca de grau ímpar e de primeira classe (  Caso). Finalmente, dividindo por
Caso). Finalmente, dividindo por 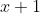 , obtemos
, obtemos
que é uma equação recíproca de grau par e de primeira classe ( forma normal ).
Considerações Finais
Conforme vimos neste artigo, qualquer equação recíproca pode ser reduzida à forma normal. Portanto, para resolvê-las, é necessário apenas saber solucionar as equações recíprocas de grau par e de primeira classe.
No próximo e último artigo desta série, nos concentraremos apenas na resolução de equações recíprocas simplificadas na forma normal.
Referência bibliográfica:
Matemática, Terceiro Ano Colegial, Ary Quintella, Companhia Editora Nacional, São Paulo, 1968.
No próximo e último artigo desta série, nos concentraremos apenas na resolução de equações recíprocas simplificadas na forma normal.
Referência bibliográfica:
Matemática, Terceiro Ano Colegial, Ary Quintella, Companhia Editora Nacional, São Paulo, 1968.


Nenhum comentário:
Postar um comentário