Dado o polinômio de coeficientes reais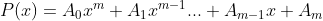 , com
, com 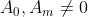 ,
, e ainda
e ainda
A equação polinomial 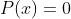 é recíproca se a mesma admite apenas raizes dos tipos
é recíproca se a mesma admite apenas raizes dos tipos  e
e 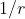 , ambas com o mesmo grau de multiplicidade
, ambas com o mesmo grau de multiplicidade  (repetições).
(repetições).
Exemplos
A equação quadrática
é recíproca porque suas raízes 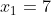 e
e 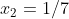 são recíprocas ou inversas.
são recíprocas ou inversas.
A equação cúbica
também é recíproca, porque duas de suas raízes 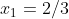 ,
, 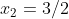 são recíprocas, sendo que a terceira raiz
são recíprocas, sendo que a terceira raiz 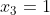 assume individualmente a forma inversa
assume individualmente a forma inversa 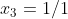 .
.
A equação de
é outro exemplo de equação recíproca, porque, conforme a definição,
possui as raízes recíprocas 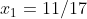 e
e 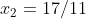 , com mesma multiplicidade
, com mesma multiplicidade 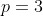 ;
;
possui as raízes inversas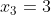 e
e 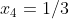 , com mesma multiplicidade
, com mesma multiplicidade 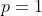 ; e
; e
possui as raízes recíprocas 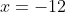 e
e 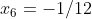 , com mesma multiplicidade
, com mesma multiplicidade 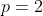 .
.
Condições para que uma equação polinomial seja recíproca
Teorema. Se uma equação polinomial é recíproca, então os coeficientes dos termos equidistantes dos extremos são
a) iguais - equações recíprocas de primeira classe
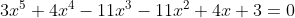
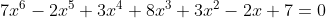
b) ou simétricos-equações recíprocas de segunda classe.
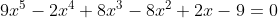
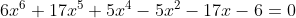
 Segue que toda equação recíproca de segunda classe e de grau par é desprovida do termo médio. No nosso último exemplo, observem que não existe o termo cúbico.
Segue que toda equação recíproca de segunda classe e de grau par é desprovida do termo médio. No nosso último exemplo, observem que não existe o termo cúbico.
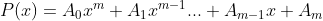
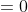 (1)
(1)
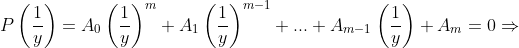
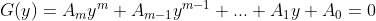 (2)
(2)
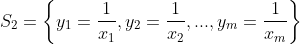
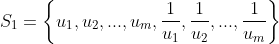
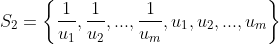
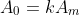
a) iguais - equações recíprocas de primeira classe
Exemplos
Exemplos
Demonstração ( teorema ). Considere uma equação polinomial qualquer, com 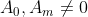 :
:
Fazendo a transformação 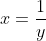 (transformada em raízes inversas ), obtemos
(transformada em raízes inversas ), obtemos
ou seja, para obter a transformada em raízes inversas de (1), basta apenas inverter a ordem dos coeficientes da equação original e colocá-las nas potências da nova variável  .
.
Enquanto as raízes de (1) são 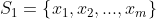 , as raízes de (2) são
, as raízes de (2) são
Mas, se a equação (1) for recíproca, suas raízes serão da forma
enquanto as raízes da transformada (2) serão
Ora, isto implica que 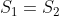 . Desta forma, uma transformação do tipo
. Desta forma, uma transformação do tipo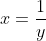 em uma equação recíproca não chega a alterá-la, pois a mesma permanecerá equivalente (mesmas raízes ) à equação original.
em uma equação recíproca não chega a alterá-la, pois a mesma permanecerá equivalente (mesmas raízes ) à equação original.
Sabemos que equações polinomiais equivalentes são da forma 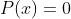 e
e 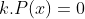 , com
, com 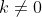 . Logo, sendo (1) recíproca, temos que os coeficientes de (2) diferem dos coeficientes de (1) apenas por um valor constante não-nulo
. Logo, sendo (1) recíproca, temos que os coeficientes de (2) diferem dos coeficientes de (1) apenas por um valor constante não-nulo  . Assim,
. Assim,
.............................
Substituindo a última igualdade na primeira, temos 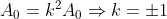 .
.
Portanto, em uma equação recíproca, os coeficientes dos termos equidistantes dos extremos são iguais ou simétricos, o que queríamos provar.
Se 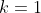 , as equações recíprocas são de primeira classe;
, as equações recíprocas são de primeira classe;
Se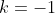 , as equações recíprocas são de segunda classe.
, as equações recíprocas são de segunda classe.
Corolário. Vamos ver agora uma prova simples de que a equação recíproca de segunda classe e grau par é desprovida do termo médio
Se a equação recíproca é de grau par, ou seja, 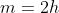 , haverá um termo central de coeficiente
, haverá um termo central de coeficiente 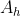 . Assim pelo teorema, temos
. Assim pelo teorema, temos 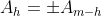 . Mas como o termo é central,
. Mas como o termo é central, 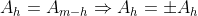 . Sendo
. Sendo 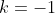 (segunda classe), esta igualdade fica
(segunda classe), esta igualdade fica 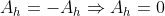 .
.
Referência bibliográfica:
Matemática, Terceiro Ano Colegial, Ary Quintella, Companhia Editora Nacional, São Paulo, 1968.
Matemática, Terceiro Ano Colegial, Ary Quintella, Companhia Editora Nacional, São Paulo, 1968.


Poxa muito legal Parabéns
ResponderExcluirOlá, Lino Lanhoso!
ResponderExcluirSeja bem vindo e obrigado!
Abraços!
Muito bom!
ResponderExcluirParaens
muito bom. PARABÉNS!
ResponderExcluir