O gráfico da função 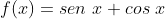 é parecido com o gráfico das funções componentes
é parecido com o gráfico das funções componentes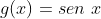 e
e  . Mas, parecido não quer dizer semelhante e embora as três funções tenham o mesmo domínio
. Mas, parecido não quer dizer semelhante e embora as três funções tenham o mesmo domínio 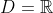 e mesmo período
e mesmo período  ,
,  difere destas outras, ponto à ponto.
difere destas outras, ponto à ponto.
Nos concentraremos em três aspectos de :
:
Nos concentraremos em três aspectos de
A) Imagem
B) Pontos críticos
C) Intersecção com os eixos coordenados
A) Imagem
Conjunto-imagem, imagem ou contra-domínio de uma função são os valores em 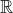 que a variável dependente
que a variável dependente 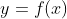 pode assumir.
pode assumir.
Tanto a imagem de
Os valores máximo total e mínimo total de uma função periódica são os limites do intervalo que definem a sua imagem. Portanto, temos que calcular o máximo e mínimo totais de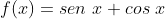 .
.
Como nestes pontos a derivada se anula, inicialmente fazemos
Como nestes pontos a derivada se anula, inicialmente fazemos
e observamos que esta igualdade ocorre nos  e
e 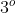 quadrantes do ciclo trigonométrico para valores de
quadrantes do ciclo trigonométrico para valores de  cíclicos de
cíclicos de 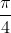 ou cíclicos de
ou cíclicos de 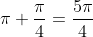 , ou seja,
, ou seja,
ou
Logo, o valor máximo e mínimo totais de
B) Pontos Críticos
Conforme vimos, os pontos máximos da função são os pontos da forma
e os pontos mínimos são os pontos da forma
Mesclando e ordenando estes valores, as abcissas dos máximos e mínimos da função
sendo que, nessa mostragem, inicia-se com a abcissa do ponto mínimo e termina com a abcissa do ponto máximo.
Calculando as abcissas e ordenadas dos pontos críticos em números decimais, por exemplo, 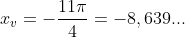 e
e 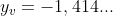 , chegamos aos seguintes valores:
, chegamos aos seguintes valores:
Confiram este resultado, assim como todos os posteriores, arrastando a bolinha azul com a seta do mouse no gráfico do google neste link: GRÁFICO DE f(x)=sen x + cos x .


C) Intersecção com os Eixos Coordenados
A intersecção da função
Já a intersecção de
e observamos que esta igualdade ocorre nos 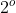 e
e 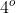 quadrantes do ciclo trigonométrico para valores de
quadrantes do ciclo trigonométrico para valores de  cíclicos de
cíclicos de 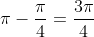 ou cíclicos de
ou cíclicos de 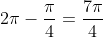 , ou seja,
, ou seja,
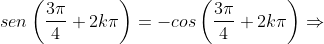
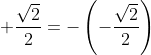
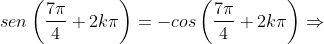
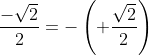
Agora vejam, ainda no ciclo trigonométrico que, da raiz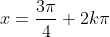 para a raiz
para a raiz 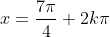 , temos um intervalo angular de
, temos um intervalo angular de 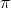 , tanto no sentido horário quanto no anti-horário. Logo, o conjunto-solução da equação
, tanto no sentido horário quanto no anti-horário. Logo, o conjunto-solução da equação  é
é

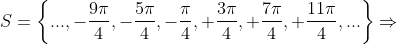
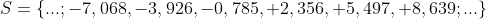
ou
Agora vejam, ainda no ciclo trigonométrico que, da raiz
( valores aproximados )
Gostará de ler também:
028-Gráficos Cartesianos Algébricos
042-Área de Intersecção Circular-Raios Iguais
099-Estudo da Função f(x)=s^(2k+1)+c^(2k+1)
Referência bibliográfica:
-Fundamentos de Matemática Elementar V1-Conjuntos-Funções, Atual Editora,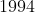 ;
;
-Fundamentos de Matemática Elementar V4-Trigonometria, Atual Editora,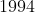 .
.
Já temos bastante informação sobre a função 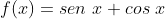 de forma que, ao esboçar seu gráfico com os dados conseguidos, perceberemos nitidamente quais os intervalos de crescimento e decrescimento, assim como os intervalos onde a função é positiva ou negativa. Vejam:
de forma que, ao esboçar seu gráfico com os dados conseguidos, perceberemos nitidamente quais os intervalos de crescimento e decrescimento, assim como os intervalos onde a função é positiva ou negativa. Vejam:
_*_
Em um futuro artigo, estudaremos a função =sen^3%20\%20x+cos^3%20\%20x) . Vejam um leve esboço do seu gráfico (proposta convertida em um estudo genérico para potências ímpares no post 099 ):
. Vejam um leve esboço do seu gráfico (proposta convertida em um estudo genérico para potências ímpares no post 099 ):
Gostará de ler também:
028-Gráficos Cartesianos Algébricos
042-Área de Intersecção Circular-Raios Iguais
099-Estudo da Função f(x)=s^(2k+1)+c^(2k+1)
Referência bibliográfica:
-Fundamentos de Matemática Elementar V1-Conjuntos-Funções, Atual Editora,
-Fundamentos de Matemática Elementar V4-Trigonometria, Atual Editora,





E como ficaria f(x) = [sen(x) + 1][cos(x) + 1]?
ResponderExcluirMuito bom, esse blog! rsrs
ResponderExcluirAmeii
ResponderExcluirGostaria de uma ideia para contextualizar essa aplicação para uma turma da segunda série do ensino médio.
ResponderExcluir