A equação do círculo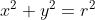 
, de centro na origem e raio 
, gera duas funções cujas representações no plano cartesiano são as seguintes: para a função 
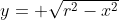temos o semicírculo mostrado no diagrama na parte superior do eixo 
. Já para a função 
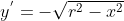temos o semicírculo na parte inferior do mesmo eixo.
Com a intenção de utilizar o Cálculo Integral para calcular a área 
do círculo, vamos utilizar a primeira função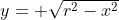 
no intervalo 
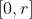. É suficiente, pois a àrea referida é quatro vezes a área sob esta curva no 
quadrante . Logo,
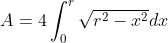
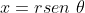
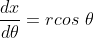
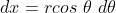
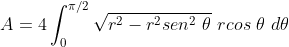
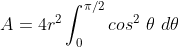
%20\%20d\theta "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
\right-2r^2\left(0-\frac{sen%20\%200}{2}\right)%20\right%20] "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
-0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
^2} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
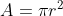
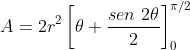
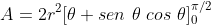
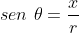
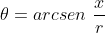
^2}\right]_0^r "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
^2}\right)-2r^2%20\left(arcsen%20\%20\frac{0}{r}+%20\frac{0}{r}\sqrt{1-\left(\frac{0}{r}\right)^2}\right) "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
-0 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
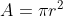
Área do Círculo com Integral:
http://manthanos.blogspot.com.br/2011/10/area-do-circulo-uma-demonstracao.html
Área do Círculo com Limites:
http://obaricentrodamente.blogspot.com.br/2009/08/demonstracao-da-area-do-circulo.html
Fazendo,
temos,
Mas,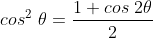 
e, substituindo, vem
Logo, o valor da nossa integral definida é
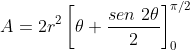
É claro que também poderíamos chegar a este resultado usando a variável 
, no lugar de 
, pelo menos na última etapa. Observem que
E revertendo a transformação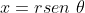, temos
Logo,
Gostará de ler também:
Referências na net:
Área do Círculo com Integral:
http://manthanos.blogspot.com.br/2011/10/area-do-circulo-uma-demonstracao.html
Área do Círculo com Limites:
http://obaricentrodamente.blogspot.com.br/2009/08/demonstracao-da-area-do-circulo.html
Mais uma postagem de qualidade...Complementa o cálculo do comprimento da circunferência.
ResponderExcluirNeste caso existe outras saídas também interessantes.Vou citar uma:
Se tomarmos o vetor de incremento linear do cilindro em função dos parâmetros (ρ,φ,z), temos:
dL= dρ ρ + ρdφ φ+ dz z
A área lateral é dada fazendo ρ=r=cte,0≤φ≤2π, e 0≤z≤h onde não há incremento dρ (Óbvio, apenas duas dimensões podem variar para o cálculo de áreas):
S(lateral)=∫ρdφ∫dz=r[φ][z]=2πrh
E a área do topo (S(topo)) e a área da base (S(base)) é dada por 0≤φ≤2π e 0≤ρ≤r, sem considerar o incremento em z.Isto é dz=0.
S(base)=S(topo)=∫dρ∫ρdφ=[ρ²/2][φ]=πr²
Daí se pode calcular a seção meridiana do cilindo (fazendo φ=cte).Enfim,também é uma boa solução.
Abraços, Aloisio.
Oi, Diogo!
ResponderExcluirSe puder enviar por e-mail (teixeira.aloisio@gmail.com) um artigo de sua autoria com esta abordagem do cálculo da área do círculo, teria prazer em publicar, com sua autorização.
Caso aceite, sugiro que use o gerador de fórmulas http://www.codecogs.com/latex/eqneditor.php. Copie e cole as fórmulas direto no e-mail.
Valeu, obrigado!
Olá novamente,Aloisio.
ResponderExcluirEntão,seria um prazer contribuir...Vou escrever utlizando este gerador de fórmulas e lhe enviar, ficando a seu critério toda e qualquer modificação.
Abraços.
Olá Aloísio,
ResponderExcluirQue bom que resolveu fazer esta publicação. Muito bacana mesmo. Ficou muito bem explicado e mais uma ótima referência na net.
Aqui tem uma demonstração por limites:
http://obaricentrodamente.blogspot.com.br/2009/08/demonstracao-da-area-do-circulo.html
Abraços.
Kleber!
ResponderExcluirObrigado! Já referenciei seu interessante artigo.
Valeu!
Olá Aloísio. Parabéns pela postagem. Na parte inicial, quando você mudou a variável, foi uma ótima sacada alterar os limites de integração para não ter que voltar pro x... simplificou bastante as coisas! Obrigado por citar o BLOG MANTHANO.
ResponderExcluirAbraço.
Pedro R.
Oi, Pedro!
ResponderExcluirObrigado!
Mas acho que a maneira mais inteligente de usar a integral para a área do Círculo é o processo de somar infinitas coroas circulares e concêntricas. Se a largura de cada coroa tender a zero, então o comprimento do círculo MENOR é tenderá ao comprimento do círculo MAIOR. Daí temos um "cilindro" de comprimento 2(pi)w (onde w vai do centro à junção dos círculos maior e menor ) e largura dr. Assim, a área deste cilindro é dA=2(pi)w.dr. Logo, dA/dr=2(pi)w. Integrando, obtemos A=(pi)w^2. Taí a explicação porque 2(pi)R é a derivada de (pi)R^2...
Valeu!
Este comentário foi removido pelo autor.
ResponderExcluirConcordo com o Aloísio... somar a área das coroas torna tudo muuuito mais fácil. Só não entendi pq ele usou o termo "cilindro" ao se referir à área de cada coroa. Uma outra forma de explicar seria:
ResponderExcluirQuando a largura das coroas tendem a zero (dr) elas se tornam anéis, suas áreas se tornam a circunferência dos anéis (2pi*r), e a soma se torna uma integral definida: S[0-R] 2pi*r dr
S[0-R] 2pi*r dr
2pi S[0-R] r dr
2pi [0-R][r^/2]
2pi*r^2/2
pi*r^2
E em 5 linhas resolve-se o problema, sem nenhuma mudança de coordenada nem relacao trigonométrica.
Achei um vídeo com essa solução: http://www.youtube.com/watch?v=la6x5YLucmw
x=rsen(teta)? Não seria x=rcos(teta) na substituição?
ResponderExcluirFaltou as passagens em que são substituídas por identidades trigonométricas. Quem não conhece talvez não consiga visualizar. No mais parabéns.
ResponderExcluir