O que tem em comum entre a expressão do enésimo termo de uma
e a fórmula de Taylor para polinômios
Resposta: é que as duas fórmulas são apenas casos particulares de ( fórmula
Onde
é o quociente de Newton . Aqui chamarei de derivada 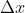 . Logo,
. Logo, 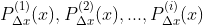 são as derivadas
são as derivadas 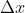 sucessivas de
sucessivas de 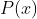 . Aqui o nome "sucessivo" tem o mesmo significado empregado com a derivada infinitesimal, com a exceção que, em lugar do incremento ter apenas a possibilidade de tender para zero (
. Aqui o nome "sucessivo" tem o mesmo significado empregado com a derivada infinitesimal, com a exceção que, em lugar do incremento ter apenas a possibilidade de tender para zero (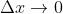 ), temos que
), temos que 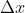 pode ser qualquer valor real diferente de zero.
pode ser qualquer valor real diferente de zero.
Assim, o enésimo termo de uma 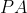 teríamos para
teríamos para 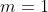 e
e 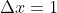 e a fórmula de Taylor para polinômios sairia para
e a fórmula de Taylor para polinômios sairia para 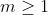 e
e 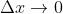 .
.
Além disso, se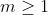 e
e 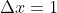 , teríamos a fórmula do enésimo termo de uma progressão aritmética de ordem
, teríamos a fórmula do enésimo termo de uma progressão aritmética de ordem  , conforme o artigo 002 .
, conforme o artigo 002 .
Além disso, se
O presente artigo tem como finalidade demonstrar a fórmula 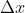 . Para isto, nos apoiaremos nos seguintes lemas.
. Para isto, nos apoiaremos nos seguintes lemas.
Lema 1. A derivada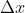 de uma soma de funções é a soma das derivadas
de uma soma de funções é a soma das derivadas 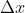 das funções, ou seja
das funções, ou seja
Lema 1. A derivada
Lema  . A derivada
. A derivada 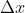 de uma constante
de uma constante  é
é  .
.
Lema 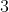 . A derivada
. A derivada 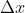 do binômio
do binômio 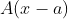 é
é  .
.
Lema
Demonstração. Seja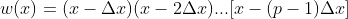 . Aplicando pontualmente a regra de derivação
. Aplicando pontualmente a regra de derivação 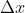 ,
,  em
em 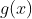 , temos que
, temos que
Mas também 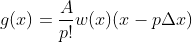 , portanto
, portanto
Logo,
TEOREMA. ( Fórmula 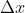 ) Dado o número real
) Dado o número real 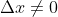 , qualquer polinômio
, qualquer polinômio 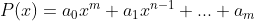 pode ser representado pela expressão
pode ser representado pela expressão
Demonstração. Como este é um teorema de existência, é necessário apenas provar a existência dos coeficientes 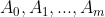 nessa disposição algébrica para provar a existência da mesma.
nessa disposição algébrica para provar a existência da mesma.
Usando o lema  , temos
, temos
Usando os lemas 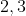 e
e 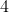 , segue
, segue
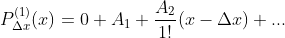
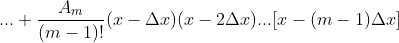
Desta forma, contando com as derivadas  sucessivas de
sucessivas de 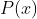 , temos
, temos
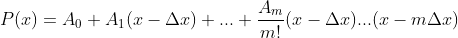
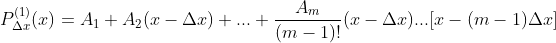
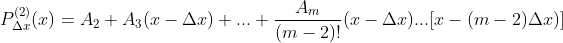 ......................................................................................................
......................................................................................................

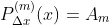
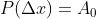
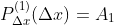
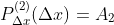
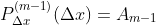
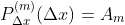
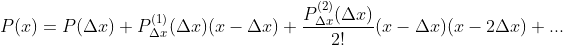
}(x)}{m!}(x-\Delta%20x)(x-2\Delta%20x)...(x-m\Delta%20x))
De forma que
.........................
Finalmente, substituindo estes valores de coeficientes em (1), temos
Conclusão: os coeficientes de (1) existem e são as derivadas 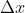 sucessivas de
sucessivas de 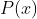 para
para 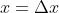 . Logo, para um mesmo polinômio
. Logo, para um mesmo polinômio 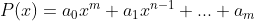 , temos infinitas representações como fórmula
, temos infinitas representações como fórmula 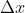 para infinitos valores de
para infinitos valores de 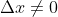 .
.
Gostará de ler também:


Olá, Aloísio!!!!
ResponderExcluirParabéns, pelas ótimas postagens que você faz e... através das suas demonstrações valiosas, além das suas preciosas observações, nos remete a um estado reflexivo sobre esses nossos conhecimentos adqueridos e considerados complexos e não guardando tão estreita ligação com outros conteúdos, coisa que você prova de maneira espetacular!!!!
Muito bom e... muito bem, grande parceiro!!!! Muita sorte da nossa parte em tê-lo aqui conosco na luta pela compreensão e domínio da ciência dos números!!!!
Um abraço!!!!!
Oi, Valdir!
ResponderExcluirObrigado. Esta fórmula Delta x descobri na adolescência em uma época que o único meio de publicação eficaz era o livro.
Por muito tempo tentei sem sucesso uma fórmula semelhante onde o incremento Delta x, no lucar de ser uma constante, varie como uma progressão aritmética ordinária. A luta seria para uma lei que forneceria os coeficientes em
P(x)=A0+A1(x-Dx)+A2(x-Dx)(x-4Dx)+A3(x-Dx)(x-4Dx)(x-9Dx), etc
Valeu, parceiro.
Abraços!