Considerações iniciais
Seja
Para 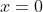 , temos
, temos 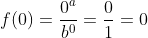 . Logo, o ponto
. Logo, o ponto 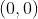 pertence ao gráfico, ou seja, a curva passa pela origem.
pertence ao gráfico, ou seja, a curva passa pela origem.
Valores para 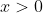
Neste caso, ambas as funções
Onde 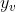 é o valor máximo de
é o valor máximo de 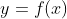 , neste intervalo. Notem que a curva intercepta o eixo
, neste intervalo. Notem que a curva intercepta o eixo 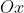 à esquerda no ponto
à esquerda no ponto 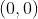 . Mas, à direita, a curva nunca intercepta o eixo horizontal, por menor que seja
. Mas, à direita, a curva nunca intercepta o eixo horizontal, por menor que seja  positivamente.
positivamente.
Valores para 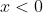
Seja
1)  ímpar.
ímpar.
Logo, 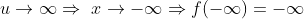
2)  par.
par.
Logo, 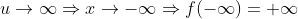
Portanto, o gráfico geral de 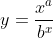 tem um dos seguintes aspectos.
tem um dos seguintes aspectos.
Domínio e imagem
Coordenadas do ponto máximo local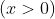
Seja 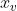 a abcissa do ponto máximo ou
a abcissa do ponto máximo ou 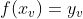 . Logo,
. Logo, 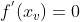 é a derivada de
é a derivada de  no ponto
no ponto 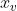 . Calculando a derivada geral da função, temos,
. Calculando a derivada geral da função, temos,
Pela regra do quociente,
Assim, 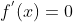 para
para 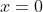 ou
ou 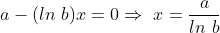 . Mas
. Mas 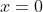 corresponde ao ponto de inflexão na origem no que concluímos que as coordenadas do ponto máximo local é
corresponde ao ponto de inflexão na origem no que concluímos que as coordenadas do ponto máximo local é
Logo, se 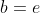 ( número de Euler), temos que o ponto máximo da função
( número de Euler), temos que o ponto máximo da função 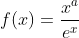 tem coordenadas
tem coordenadas 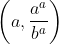 .
.
Área no intervalo
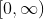
Para calcular a àrea no intervalo
porque, de posse deste resultado, basta fazer 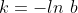 e calcular o valor da integral nos limites do intervalo considerado.
e calcular o valor da integral nos limites do intervalo considerado.
Usaremos a fórmula de integração por partes 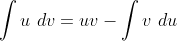 com a idéia de reduzir a integral (1)
à uma outra que contenha uma potência de menor grau e assim por diante,
até o grau da potência ser zero e, a partir daí, operá-la como uma
constante.
com a idéia de reduzir a integral (1)
à uma outra que contenha uma potência de menor grau e assim por diante,
até o grau da potência ser zero e, a partir daí, operá-la como uma
constante.
Sejam
Inserindo estes resultados na fórmula,
Por sua vez,
Substituindo (3) em (2),
Por sua vez,
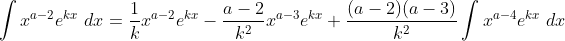 (5)
(5)
Substituindo (5) em (4),
Podemos induzir que,
sendo 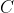 a constante de integração.
a constante de integração.
Agora, dado  , com
, com 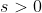 , seja
, seja 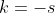 e considere
e considere 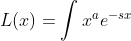 .
.
Neste caso, verifiquem no segundo membro de (6) que, se 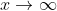 , temos
, temos
E para 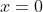 , temos
, temos 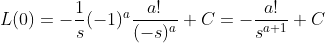
Assim, 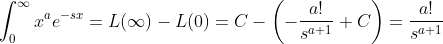 (7)
(7)
Logo, para calcularmos a área
_*_
Referência Bibliográfica:
- Manual de Fórmulas e Tabelas Matemáticas, Coleção Schaum, ![3^a [;3^a;]](http://thewe.net/tex/3^a) edição, de Murray R.Spiegel, Seymour Lipschutz e John Liu, Ed.Bookman,
edição, de Murray R.Spiegel, Seymour Lipschutz e John Liu, Ed.Bookman, ![2011 [;2011;]](http://thewe.net/tex/2011) ;
;
-Transformadas de Laplace, Coleção Schaum, de Murray R.Spiegel, Ed.McGRAW-HILL, ![1965 [;1965;]](http://thewe.net/tex/1965) .
.
Referência na net:
http://fatosmatematicos.blogspot.com.br/2011/06/integral-do-produto-da-exponencial-pela.html
Referência na net:
http://fatosmatematicos.blogspot.com.br/2011/06/integral-do-produto-da-exponencial-pela.html





Parabéns pelo post. Muito interessante este estudo da função definida pela razão entre a função potencial e a exponencial. Na parte que trata da integral, lembrei que eu também escrevi algo semelhante neste link
ResponderExcluirhttp://fatosmatematicos.blogspot.com.br/2011/06/integral-do-produto-da-exponencial-pela.html
Obrigado, Paulo!
ResponderExcluirComo curiosidade, coloque no Geogebra ou programa similar a função [;y=b^x/x^a;] ( a inversa ) e veja que temos um novo aspecto gráfico que, se não for útil para alguma coisa, pelo menos seria divertido uma análise.
Deixei um comentário no seu artigo referido.
Valeu!
Adicionei um link deste post no post que eu escrevi. Até mais.
ExcluirMais um exelente post de um ótimo blog
ResponderExcluirAloisio vc comanda um blog mega interessante e gostaria de ter parabens por ste belíssimo blog
Oi, Matheus!
ResponderExcluirObrigado pela consideração!
Um abraço e volte sempre!