Giovanni Domenico Cassini ( ) foi um astrônomo e matemático italiano que, nas suas tentativas de compreender o movimento dos corpos celestes, apresentou estranhas curvas como alternativas às trajetórias elípticas de Kepler (
) foi um astrônomo e matemático italiano que, nas suas tentativas de compreender o movimento dos corpos celestes, apresentou estranhas curvas como alternativas às trajetórias elípticas de Kepler (  ).
).
Como estudamos no ensino médio, em uma elipse, a soma da distância de um ponto da mesma a um de seus focos com a distância deste mesmo ponto ao outro foco é constante.
Cassini supôs que, em um movimento orbital de um astro, em torno de dois focos, no lugar de pensar na soma, seria o produto das distâncias consideradas anteriormente que seria constante.
Neste último caso, a equação resultante gera curvas que ficaram conhecidas como ovais de Cassini, mesmo que nem sempre tenham o aspecto sugerido.
A lemniscata de Bernoulli é um caso particular de oval de Cassini, embora dificilmente se possa imaginar um planeta com tal trajetória.
Vamos calcular, agora, a equação de um ponto que descreve uma trajetória cujo produto das distâncias deste ponto à dois focos fixados seja sempre constante ( como sugerido por Giovanni Cassini).
Considere o diagrama a seguir.
No diagrama, os pontos ![F_2(-a,0) [;F_2(-a,0);]](http://thewe.net/tex/F_2(-a,0)) e
e ![F_1(a,0) [;F_1(a,0);]](http://thewe.net/tex/F_1(a,0)) são fixados ao longo do eixo
são fixados ao longo do eixo ![Ox [;Ox;]](http://thewe.net/tex/Ox) simetricamente em relação a origem
simetricamente em relação a origem ![O [;O;]](http://thewe.net/tex/O) . Os mesmos são os focos da curva que queremos equacionar.
. Os mesmos são os focos da curva que queremos equacionar.
Considere o ponto ![P [;P;]](http://thewe.net/tex/P) móvel em relação à origem
móvel em relação à origem ![O [;O;]](http://thewe.net/tex/O) . Sua coordenada polar é
. Sua coordenada polar é ) enquanto sua coordenada cartesiana é
enquanto sua coordenada cartesiana é ![(x,y) [;(x,y);]](http://thewe.net/tex/(x,y)) .
.
O padrão de movimento de ![P [;P;]](http://thewe.net/tex/P) é tal que
é tal que ![d_1.d_2=k=cte [;d_1.d_2=k=cte;]](http://thewe.net/tex/d_1.d_2=k=cte) .
.
Nestas condições, qual a equação que descreve a trajetória de ![P [;P;]](http://thewe.net/tex/P) ?
?
Para começar, usaremos a lei dos cossenos duas vezes. Primeiro para expressar ![d_1 [;d_1;]](http://thewe.net/tex/d_1) no triângulo
no triângulo ![POF_1 [;POF_1;]](http://thewe.net/tex/POF_1) e depois para expressar
e depois para expressar ![d_2 [;d_2;]](http://thewe.net/tex/d_2) no triângulo
no triângulo ![POF_2 [;POF_2;]](http://thewe.net/tex/POF_2) .
.
Assim, -(2ar.cos%20\%20\theta)][(r^2+a^2)+(2ar.cos%20\%20\theta)]%20\Rightarrow)
Mas, 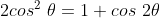 .Substituindo,
.Substituindo,
Esta é a equação polar das ovais que pode ser simplificada na seguinte situação particular.
Observando novamente o diagrama
Observando novamente o diagrama
 vejam que no caso do ponto
vejam que no caso do ponto
Voltaremos a esta forma reduzida mais a frente.
Colocaremos (1) agora nas variáveis![x [; x;]](http://thewe.net/tex/ x) e
e ![y [;y;]](http://thewe.net/tex/y) . Já que
. Já que ![r^2=x^2+y^2 [;r^2=x^2+y^2;]](http://thewe.net/tex/r^2=x^2+y^2) ,
, 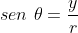 e
e  , temos
, temos
Colocaremos (1) agora nas variáveis
que é a equação cartesiana das ovais de Cassini. Temos três casos a considerar referente ao produto ![k=d_1d_2=cte [;k=d_1d_2=cte;]](http://thewe.net/tex/k=d_1d_2=cte) :
:
a) ![k>a^2 [;k>a^2;]](http://thewe.net/tex/k%3Ea%5E2)
b) ![k=a^2 [;k=a^2;]](http://thewe.net/tex/k=a%5E2)
c) ![k<a^2 [;k<a^2;]](http://thewe.net/tex/k<a^2)
Estes três casos originam três formatos da tragetória do ponto ![P [;P;]](http://thewe.net/tex/P) ou curvas em estudo.
ou curvas em estudo.
Vamos aos gráficos.
a) ![k>a^2 [;k>a^2;]](http://thewe.net/tex/k%3Ea%5E2)
Temos então,

Em contrapartida, se o produto
b) ![k=a^2 [;k=a^2;]](http://thewe.net/tex/k=a%5E2)
Neste caso, temos
O gráfico passa pela origem e o equivalente polar desta equação é
Esta curva é conhecida como lemniscata de Bernoulli. James Bernoulli (
c) ![k<a^2 [;k<a^2;]](http://thewe.net/tex/k%3Ca%5E2)
Aqui, temos ![(x^2+y^2)^2-2a^2(x^2-y^2)=k^2-a^4<0 [;(x^2+y^2)^2-2a^2(x^2-y^2)=k^2-a^4<0;]](http://thewe.net/tex/(x^2+y^2)^2-2a^2(x^2-y^2)=k^2-a^4<0) . Ocorre um curioso fenômeno geométrico. É como se a origem cortasse o "oito deitado" o dividindo em duas partes simétricas em relação ao eixo
. Ocorre um curioso fenômeno geométrico. É como se a origem cortasse o "oito deitado" o dividindo em duas partes simétricas em relação ao eixo ![Oy [;Oy;]](http://thewe.net/tex/Oy) . Cada parte tem um aspecto oval. E também é como se o ponto
. Cada parte tem um aspecto oval. E também é como se o ponto ![P [;P;]](http://thewe.net/tex/P) tivesse um reflexo de sua trajetória do lado esquerdo. De fato, cada ponto da parte do gráfico da esquerda também obedece a lei
tivesse um reflexo de sua trajetória do lado esquerdo. De fato, cada ponto da parte do gráfico da esquerda também obedece a lei ![d_1d_2=k(cte)<a^2 [;d_1d_2=k(cte)<a^2;]](http://thewe.net/tex/d_1d_2=k(cte)<a^2) .
.
Quando ![k=d_1d_2=k(cte)<a^2 [;k=d_1d_2=k(cte)<a^2;]](http://thewe.net/tex/k=d_1d_2=k(cte)<a^2) tender para zero, ou seja, quando
tender para zero, ou seja, quando 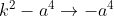 então os aspectos ovais se retrairão, um para a esquerda e o outro para a direita, onde cada um diminuirá de tamanho, ficando cada vez mais parecido com um círculo cujo centro é o seu respectivo foco.
então os aspectos ovais se retrairão, um para a esquerda e o outro para a direita, onde cada um diminuirá de tamanho, ficando cada vez mais parecido com um círculo cujo centro é o seu respectivo foco.
Até que, quando ![k=0 [;k=0;]](http://thewe.net/tex/k=0) , ou seja,
, ou seja, ![(x^2+y^2)^2-2a^2(x^2-y^2)=-a^4 [;(x^2+y^2)^2-2a^2(x^2-y^2)=-a^4;]](http://thewe.net/tex/%28x%5E2+y%5E2%29%5E2-2a%5E2%28x%5E2-y%5E2%29=-a%5E4) , então o gráfico desta equação será apenas dois pontos sobre o eixo
, então o gráfico desta equação será apenas dois pontos sobre o eixo ![Ox [;Ox;]](http://thewe.net/tex/Ox) ( os outroras focos ).
( os outroras focos ).
 Apesar de seu equívoco no formato das órbitas, Cassini nos legou a beleza das curvas estudadas neste post. Além disso, realizou importantes trabalhos em Astronomia. Registrou a aparição de inúmeros cometas. Produziu precisas tabelas solares. Observou os períodos de rotação de Vênus, Marte e Júpiter. Quando foi nomeado diretor do Observatório Astronômico de Paris, descobriu as luas de Saturno, Jápeto e Reia em
Apesar de seu equívoco no formato das órbitas, Cassini nos legou a beleza das curvas estudadas neste post. Além disso, realizou importantes trabalhos em Astronomia. Registrou a aparição de inúmeros cometas. Produziu precisas tabelas solares. Observou os períodos de rotação de Vênus, Marte e Júpiter. Quando foi nomeado diretor do Observatório Astronômico de Paris, descobriu as luas de Saturno, Jápeto e Reia em Referência bibliográfica:
[1] Cálculo com Geometria Analítica, volume
[2] Curvas Notáveis, de A.I.Markuchevitch, Atual Editora,
Referência na Net:
http://pt.wikipedia.org/wiki/Giovanni_Domenico_Cassini
Gostará de ler também:
101-Estudo da Função f(x)=x^a/b^x
099-Estudo da Função f(x)=s^(2k+1)+c^(2k+1)
087-Estudo da Função f(x)=sen x +cos x
042-Área de Intersecção Circular-Raios Iguais
028-Gráficos Cartesianos Algébricos







Post muito bem elaborado, uma verdadeira aula de Geometria Analítica e História da Matemática. Certa vez rascunhei alguma coisa sobre as ovais de Cassini, mas reconheço uue este post ficou muito melhor do que minhas ideias rascunhadas. Parabéns.
ResponderExcluirOi, Paulo!
ExcluirEstas curvas são bem interessantes mesmo. E se no lugar do produto constante, fosse a divisão constante? E como seriam sua versões em 3D? Ainda estou na estaca zero em figuras espaciais.
Obrigado pelo comentário.
Um abraço!
Olá Aloísio, que maravilha, não? Este estudo que fez ficou muito bom, analisando os valores de k separadamente podemos ver seu comportamento gráfico. As imagens estão muito bem elaboradas, o que facilita bastante o entendimento. Como é interessante a matemática: às vezes de um problema, surgem novas teorias, daí sua beleza. Apesar de estar errado na sua teoria das órbitas, podemos ver que Cassini foi muito importante para a astronomia e matemática, tanto é verdade que hoje temos a sonda Cassini-Huygens orbitanto Saturno.
ResponderExcluirGrande abraço!
Obrigado, Kleber!
ExcluirEssas viagens espaciais são todas frutos da matemática como pode-se notar pelo nome duplo da sonda que mencionou.
Respondendo a minha última pergunta acima, veja este site: http://paulbourke.net/geometry/egg/
Abraços!
Quando li sua questão, imaginei que fosse assim mesmo, sólidos de revolução, obtidos quando tais curvas são rotacionadas em torno do eixo dos x. Acho que a teoria será fácil para você, só tem que usar um software para gerar as curvas em 3d.
ResponderExcluirQuando fiz aquelas construções de ovos de galinha, tinha salvo estas páginas:
http://www.mathematische-basteleien.de/eggcurves.htm
http://www16.ocn.ne.jp/~akiko-y/Egg_by_Itou/index_egg_by_Itou_E.html
trata de ovais, bem legal.
Achei este site que gera gráficos online>
http://cose.math.bas.bg/webMathematica/MSP/Sci_Visualization/3DFunctionPlot.msp
Entre com a função e pressione o botão "EvaluateStatic" para gerar o gráfico.
Vou procurar como fazer na Wolfram Alpha. O Paulo deve saber. Veja nos links:
http://fatosmatematicos.blogspot.com.br/2011/11/superficies-parametricas-atraves-do.html
http://fatosmatematicos.blogspot.com.br/2012/01/superficies-parametricas-atraves-do.html
Abraços!
Valeu pelas dicas, Kleber! Vi que nos dois primeiros sites possuem equações e gráficos bem exóticos, na sua maioria ovais.
ExcluirNeste ano vou explorar o W.A. pois notei que as figuras ficaram excelentes no blog do Paulo.
Valeu!
Na passagem da equação (1) da lemniscata de Bernoulli para a forma reduzida (2) dividiu-se ambos os membros da equação (1) por r^2.Mas nesse caso, considerando o ponto P na origem O, sua coordenada polar r é nula, logo acho que não poderia haver tal simplificação.Se eu estiver enganado me corrija, por favor.
ResponderExcluirBem observado, Unknown. Na equação reduzida, o gráfico é um "oito deitado". Observe que possui infinitos pontos distintos da origem, onde a fórmula simplificada, com o cancelamento de r^2, funciona. Mas observe também que se inserirmos (0,0) na fórmula, ela também funcionará. Dizemos então que, neste ponto, a fórmula é simplificada com o corte dos r^2, quando r tende a zero, como se fosse um limite. Espero ter esclarecido.
ExcluirEntendi...Mas o produto d1d2=a^2 vale para todos os pontos da curva ou somente quando se considera o ponto na origem?
Excluird1.d2=a^2 é a condição que gera toda a curva, por corolário de definição. Portanto, vale para todos os pontos.
ResponderExcluirEstava a procura de informações sobre a Lemniscata de Bernoulli quando encontrei seu blog falando sobre Cassini. Foi incrível entender de forma simples e clara a explanação ofertada acima. Gostaria de deixar aqui a construção em GeoGebra das Ovais de Cassini no link https://www.geogebra.org/m/q2xexuxq. Os controles "k" e "'a" variam a constante k e as distâncias dos focos. Muito prazer.
ResponderExcluir