com 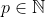 e a combinação
e a combinação  para
para 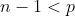
Digo que 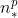 no Cálculo Discreto é o equivalente algébrico do monômio
no Cálculo Discreto é o equivalente algébrico do monômio 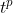 (
( 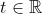 variável ) no Cálculo Infinitesimal, tendo em vista que a derivada discreta
variável ) no Cálculo Infinitesimal, tendo em vista que a derivada discreta 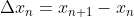 e a integral discreta
e a integral discreta 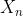 ( tal que
( tal que 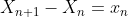 ) de
) de 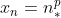 são, respectivamente
são, respectivamente
onde cada resultado tem um formato semelhante à derivada ou à integral infinitesimais de =t^p) .
.
Demonstração. Ver lema 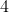 do artigo 093 . Naquele texto considere
do artigo 093 . Naquele texto considere 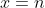 e
e 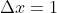 .
.
Ainda, a base e a base
e a base  ( número de Euler ) são equivalentes funcionais nos dois Cálculos em questão, porque
( número de Euler ) são equivalentes funcionais nos dois Cálculos em questão, porque
Ainda, a base
sendo que o primeiro caso é facilmente verificável usando o operador 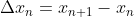 em
em 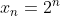 .
.
Vejam o reflexo destas equivalências nas seguintes comparações da transformada de Laplace e da Função Gama ( na função contínua

Os operadores contínuos aplicados em
Demonstração da Transformada Discreta de Laplace Base  para
para
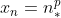
Para provar que
onde, ) é um polinômio de
é um polinômio de  -ésimo grau ;
-ésimo grau ;
Podemos considerar
As derivadas discretas consecutivas de ) são
são
.............................................................................................................
De forma que para
E, para
Notem que em todas as expressões de
E, por último, ficamos sabendo que =cte=P_p(1)=p!) (4)
(4)
Substituindo (2), (3) e (4) em (1) , temos
Finalmente, fazendo 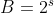 , com
, com 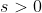 (real),
(real),
Demonstração da Função Gama Discreta
Conforme visto no quadro comparativo, a função gama discreta
que é um caso particular da transformada discreta de Laplace 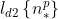 , quando
, quando 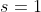 .
.
Vejamos, agora, uma prova de (5) utilizando a versão corrente da transformada discreta de Laplace 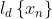 que usa a base
que usa a base 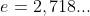 conhecida como
conhecida como 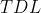 .
.
Esta versão teve sua aplicabilidade desenvolvida pelo mestre em matemática pura Prof Paulo Sérgio no seu blog fatosmatematicos.blogspot.com.br .
Usarei o caso particular da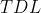 quando
quando 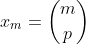 , com
, com 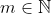 , cuja demonstração encontra-se no referido blog na proposição
, cuja demonstração encontra-se no referido blog na proposição  do artigo intitulado A TDL e Aplicações nas Equações de Recorrência.
do artigo intitulado A TDL e Aplicações nas Equações de Recorrência.
Esta versão teve sua aplicabilidade desenvolvida pelo mestre em matemática pura Prof Paulo Sérgio no seu blog fatosmatematicos.blogspot.com.br .
Usarei o caso particular da
Fazendo 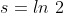 , temos
, temos
Multiplicando por 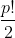 ,
,
Fazendo 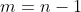 ,
,


Excelente post, gostei bastante. Temos que explorar mais esta função gama discreta. Parabéns pelo post e muito obrigado pelo link citado acima.
ResponderExcluirObrigado, Prof!
ResponderExcluirTemos que achar um significado para [;n_*^p;] quando [;p;] não for um inteiro.
Do exposto tiramos que [;\sum_{n=1}^{\infty} 2^{-n} {n \choose p}=1;]
Valeu.
Oi! Teixeira! Bom primeiramente "EU SOU AVÔ". Nasceu Pietro! O bichinho tá em casa e chora como um pavarotti, mas agora tá quietinho. Então Teixeira, sobre achar um significado para "n*p". Acho que a transformada discreta, os somatórios que você desenvolveu e a função P(n;p) (dos álbuns) devem ter tudo a ver com as funções zeta e gama, outro dia fuçando (sem demonstração) na P(n;n)=n! encontrei o valor para gama(1/2)=raiz de pi com oito casas exatas não deve ser coincidência.
ResponderExcluirMeus parabéns, amigo Tavano, pelo acréssimo familiar! Que seu neto tem saúde plena e seja tão inteligente quanto o avô!
ResponderExcluirAcho que um grande quebra-cabeça está sendo montado. Aos poucos vamos ver como tudo se encaixará.
Queria saber sobre estes seus cálculos sobre raíz de pi. Se quiser use o e-mail.
Bem, eu não tenho uma barba branca de estudos e experiências, por isso agradeço por ter nascido na Era da Informação onde as trocas de idéias são tão facilitadas...
Abraços!
Oi, Teixeira! Está pronto para assassinarmos a Matemática? Vamos lá: Escolhi o "3" que dá menos trabalho, 3!=P(3;3)=3^3 - 3(2^3) + 3X2(1^3)/2! - 3X2X1(0^3)/3!. Quanto seria 3,5!? Fiz assim 3,5!=3,5^3,5 - 3,5(2,5^3,5) + 3,5X2,5(1,5^3,5)/2! -
ResponderExcluir3,5X2,5X1,5(0,5^3,5)/3!=11,63402. Na verdade 3,5!=11,63173... Sabemos que raiz de pi=(-1/2)!=1,772453. Se dividirmos 3,5! por 3,5X2,5X1,5X0,5 obteremos (-1/2)!pela propriedade do fatorial (n+1)!=(n+1)n!. Pois é 11,63402/3,5.2,5.1,5.0,5=1,7728031..
OBS: 1)Quando fiz o mesmo acima para "7" encontrei raiz de pi com oito casas corretas
2)A "série" acima deve ter infinitos termos, caso contrário raiz de pi seria algébrico.
3)O problema de expandir mais a série acima é que entrarão números complexos do tipo [(-0,5)^3,5], e, nem sei, se será convergente.
abçs.
Oi, Tavano!
ExcluirTeve um matemático que não me recordo o nome que disse que:
"Usamos a INTUIÇÃO para descobrir a RAZÃO para demonstrar".
Sem dúvidas, na maioria das vezes a percepção vem primeiro que a compreenção.
Interessante os seus cálculos. Vou reproduzir no papel, inclusive com outros exemplos.
Um abraço!