Diagrama 1
Diagrama 2
Na geometria analítica, o teorema de Pitágoras é expressado pela fórmula da distância
Vejamos como podemos utilizar estes dois enfoques do
A estratégia para provar ) é a seguinte. Observem o diagrama diagrama
é a seguinte. Observem o diagrama diagrama 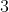 . Primeiro calcula-se a distância
. Primeiro calcula-se a distância  com as coordenadas de cada ponto. Depois transladamos o triângulo
com as coordenadas de cada ponto. Depois transladamos o triângulo 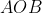 ( diagrama
( diagrama 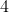 ) de forma que o ângulo
) de forma que o ângulo  fique negativo . Do mesmo jeito, calculamos novamente a distância
fique negativo . Do mesmo jeito, calculamos novamente a distância  . Então igualamos os resultados das distâncias ( já que são a mesma ) e cancelamos os termos iguais. O que sobrar é a expressão para
. Então igualamos os resultados das distâncias ( já que são a mesma ) e cancelamos os termos iguais. O que sobrar é a expressão para 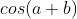 . Vamos aos cálculos.
. Vamos aos cálculos.
Diagrama 3
No diagrama 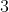 as coordenadas de
as coordenadas de  e
e  são:
são:
A distância entre  e
e  é tal que
é tal que
Diagrama 4
A distância entre
Igualando (1) com (2), temos
_*_
Para achar ) basta lembrar que
basta lembrar que =-sen(b)) ,
, =cos(b)) e fazer
e fazer
Como ) ,deixo como exercícios aos leitores as provas de que
,deixo como exercícios aos leitores as provas de que
Para finalizar, deixo um excelente vídeo do youtube sobre a demonstração tradicional para ) .Obs: para aumentar a tela cliquem no quadrado abaixo e à direita do vídeo. Ou então assistam neste link: http://www.youtube.com/watch?v=X7icfnFNA6c
.Obs: para aumentar a tela cliquem no quadrado abaixo e à direita do vídeo. Ou então assistam neste link: http://www.youtube.com/watch?v=X7icfnFNA6c






Realmente, a demostração apresentada é muito elegante: mais natural, ao meu ver, que a demonstração tradicional.
ResponderExcluirParabéns.
Oi, João Elias F.S. Rodrigues!
ResponderExcluirEstou vendo se consigo um ajuste para provar sen(a+b) sem recorrer para cos(a+b).
Obrigdo pela visita e comentário.
Um abraço