No post 107 , vimos alguns métodos para calcular o ponto máximo da curva gerada por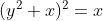 
.
Vimos também que o volume do sólido de revolução desta curva relativo ao eixo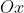 
é 
.
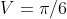O Prof. Paulo Sérgio do blog FATOS MATEMÁTICOS informou por e-mail sobre seu cálculo da área interna limitada pela curva em estudo no que resultou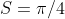 
. Daí temos duas conclusões e uma conjectura:
CÁLCULO DA ÁREA TOTAL 
LIMITADA INTERNAMENTE PELA CURVA DE EQUAÇÃO 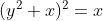ou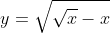 
( demonstração do Prof Paulo Sérgio de que ) .
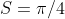Por simetria, 
Seja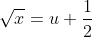
. Assim,
^2%20\Rightarrow%20dx=2\left(u+\frac{1}{2}\right)du "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
e ainda,
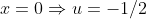
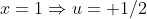
( mudança dos limites de integração )
Fazendo as substituições na integral, temos
+\left(u+\frac{1}{2}\right)^2}.2\left(u+\frac{1}{2}\right)du "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
du "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
%20\%20du "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
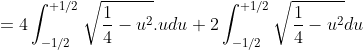
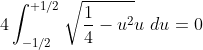
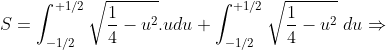
^2=\frac{\pi}{4} "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
Seja
( mudança dos limites de integração )
Fazendo as substituições na integral, temos
Temos a soma de duas integrais relativas às funções definidas por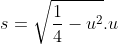 
e 
, respectivamente.
Na primeira função, devido ao fator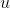 
,os valores de 
no intervalo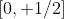 
são simétricos aos valores no intervalo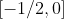 
, com exceção do ponto  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
. Consequentemente,
Já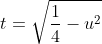 
é equivalente à ^2 "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
. Esta expressão representa um círculo na origem de raio 
. A integral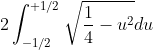 
, portanto, calcula a área do dobro da metade ( área do círculo inteiro ). Logo, o valor de fica
Olá Aloisio, ficou muito bom o post e muito obrigado pela divulgação em seu blog. Rascunhei o comprimento de arco, mas não cheguei numa integral muito difícil. Desconfio que a conjectura seja falsa.
ResponderExcluirOi, Paulo
ResponderExcluirObrigado pela colaboração. Para resolver esta integral, inicialmente eu tinha substituido x^0.5 por z, com x=z^2. No que segue dx=2z.dz. A integral ficaria nos mesmos limites 0 e 1 e o integrando 2(z-z^2)^0.5.zdz. No entanto verifiquei que a integral definida seria zero???? Depois não soube como prosseguir. Mas vejo nos seus cálculos que a substituição x^0.5=u+0.5 é mais útil.
Já para o cálculo do comprimento temos uma integral mais espinhosa. Acho que provar que não é pi seja mais viável que o cálculo direto.
Valeu!
Olá amigos.
ResponderExcluirEste artigo é para fortalecer o nosso conhecimento sobre a área lateral de um Cone reto.
Numa pesquisa recente descobrimos que a área quadrada de uma Elipse e igual à área lateral de um Cone Reto.
Conclusão:
se multiplicarmos um número por ele mesmo e depois por pi (3,14), o resultado é exatamente a área do Círculo.
Se multiplicarmos um número por outro e depois por pi (3,14), o resultado é exatamente a área de uma Elipse, ok?
De igual modo, se multiplicarmos um número por outro e depois por pi (3,14), o resultado é exatamente a área lateral de um Cone reto, ok?
Um simples raciocínio, não é mesmo?
Atenciosamente,
edinho silva.
Édison Martins da Silva.
Compartilhando conhecimentos em Matemática Avançada.
Oi, Édison.
ExcluirAgradeceria se vc tecesse um comentário a respeito do que foi publicado na presente postagem.
Acho inadequado usar este espaço para seu tema e ignorar o trabalho em vigor.
Em outras ocasiões eu te respondi e comentei favoralvemente a respeito de seus trabalhos e tenho certeza que gostou.
Se desejar transmitir algo mais, solicito usar o e-mail.
Espero que não haja nenhum mal-entendido sobre o que escrevi.
Atenciosamente.
Aloisio Teixeira