Veremos neste artigo:
Fórmulas para seno e cosseno de arcos múltiplos
Primeira identidade.
Demonstração. Levando em conta que
Somando com
Mas como \alpha]=sen(2\alpha-\alpha%20n)=sen[-(n-2)%20\alpha]=-sen[(n-2)%20\alpha]) , chegamos à
, chegamos à
Segunda identidade. =2cos[(n-1)\alpha]%20cos%20(\alpha)-cos%20[(n-2)%20\alpha])
Demonstração. Desde que %20\alpha+\alpha) , temos
, temos
Somando com %20\alpha]cos(\alpha)-cos[(n-1)%20\alpha]cos(\alpha)=0) , obtemos
, obtemos
Somatório exponencial-trigonométrico do seno
Usaremos a primeira identidade. Começaremos com
À partir da segunda parcela, colocando 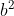 em evidência e, por sua vez,
em evidência e, por sua vez, ) em evidência, temos
em evidência, temos
Agora, adicionando e subtraindo termos dentro dos colchetes de forma que se complete ) , temos
, temos
Por fim, resolvemos a equação em ) :
:
+b^2\sum_{n=1}^n%20b^n%20sen(\alpha%20n)-2bcos(\alpha)\sum_{n=1}^n%20b^n%20sen(\alpha%20n)=)
+b^{n+1}sen[(n-1)%20\alpha]+b^{n+2}sen(n%20\alpha)+)
%20sen(n%20\alpha)%20\Rightarrow)
]\sum_{n=1}^n%20b^n%20sen(\alpha%20n)=)
+b^{n+2}sen(n%20\alpha)+b^{n+1}%20\underbrace{\left{sen[(n-1)\alpha]-2cos(\alpha)sen(n%20\alpha)%20\right}%20}_{-sen[(n+1)\alpha]}\Rightarrow)
=\frac{bsen(\alpha)-b^{n+1}sen[(n+1)\alpha]+b^{n+2}sen(n%20\alpha)}{1+b^2-2bcos(\alpha)})
Somatório exponencial-trigonométrico do cosseno
O somatório![\sum_{n=1}^n b^ncos (\alpha n) [;\sum_{n=1}^n b^ncos (\alpha n);]](http://thewe.net/tex/%5Csum_%7Bn=1%7D%5En%20b%5Encos%20%28%5Calpha%20n%29) é calculado nos mesmos moldes do anterior. Usaremos, desta vez, a identidade para
é calculado nos mesmos moldes do anterior. Usaremos, desta vez, a identidade para ) . Observem que no processo não utilizaremos de forma nenhuma a função seno.
. Observem que no processo não utilizaremos de forma nenhuma a função seno.
=bcos(\alpha)+b^2cos(2%20\alpha)+b^3cos(3%20\alpha)+...+b^ncos(n%20\alpha)=)
+)
cos(\alpha)}_{cos(2\alpha)}+)
cos(\alpha)-cos(\alpha)]+}_{cos(3%20\alpha)})
![+...+ [;+...+;]](http://thewe.net/tex/+...+)
\alpha]cos(\alpha)-cos[(n-2)\alpha]}_{cos(n%20\alpha)}=)
-)
-)
-)
%20\alpha]+)
cos(\alpha)+)
cos(\alpha)+)
cos(\alpha)+)
\alpha]cos(\alpha))
=)
-b^2[bcos(\alpha)+b^2cos(2%20\alpha)+b^3cos(3%20\alpha)+...+b^{(n-2)}cos(n-2)%20\alpha]+)
[bcos(\alpha)+b^2cos(2%20\alpha)+b^3cos(3%20\alpha)+...+b^{(n-1)}cos(n-1)%20\alpha])
=)
-b^2\left%20\{%20\sum_{n=1}^n%20b^n%20cos(\alpha%20n)-b^{n-1}cos[(n-1)\alpha]-b^n%20cos(n%20\alpha)%20\right%20\}+)
%20[\sum_{n=1}^n%20b^n%20cos(\alpha%20n)-b^n%20cos(n%20\alpha)]=)
-b^2%20\sum_{n=1}^n%20b^n%20cos(\alpha%20n)+b^{n+1}cos[(n-1)%20\alpha]+b^{n+2}cos(n%20\alpha)+)
\sum_{n=1}^n%20b^n%20cos(\alpha%20n)-2b^{n+1}cos(\alpha)%20cos(n%20\alpha))
Por fim, resolvemos a equação em ) :
:
+b^2\sum_{n=1}^n%20b^n%20cos(\alpha%20n)-2bcos(\alpha)\sum_{n=1}^n%20b^n%20cos(\alpha%20n)=)
+b^{n+1}cos[(n-1)%20\alpha]+b^{n+2}cos(n%20\alpha)+)
%20cos(n%20\alpha)%20\Rightarrow)
]\sum_{n=1}^n%20b^n%20cos(\alpha%20n)=)
+b^{n+2}cos(n%20\alpha)+b^{n+1}%20\underbrace{\left{cos[(n-1)\alpha]-2cos(\alpha)cos(n%20\alpha)%20\right}%20}_{-cos[(n+1)\alpha]}\Rightarrow)
=\frac{bcos(\alpha)-b^{n+1}cos[(n+1)\alpha]+b^{n+2}cos(n%20\alpha)}{1+b^2-2bcos(\alpha)})
Somatório exponencial-trigonométrico do cosseno
O somatório
À partir da segunda parcela, colocando 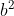 em evidência e, por sua vez,
em evidência e, por sua vez, ) em evidência, temos
em evidência, temos
Agora, adicionando e subtraindo termos dentro dos colchetes de forma que se complete ) ,temos
,temos
A transformada discreta de Laplace (
A transformada discreta de Laplace (
Temos duas versões da
A primeira consiste em multiplicar a função discreta
Na segunda versão, multiplicamos
A 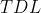 existirá, desde que seu somatório específico tenham um limite.
existirá, desde que seu somatório específico tenham um limite.
Vimos que
Base
Base
Analogamente, mas utilizando
Base ![e [;e;]](http://thewe.net/tex/e) .
. %20\right%20\}=1+\frac{e^scos%20\%201}{e^{2s}-(2cos%20\%201)e^s+1%20}\Rightarrow)
Base ![2 [;2;]](http://thewe.net/tex/2) .
. %20\right%20\}=\frac{(cos%20\%201)2^s}{4^{s}-(cos%20\%201)2^{s+1}+1%20})
Referência bibliográfica.
 Manual de Sequências e Séries - Volume
Manual de Sequências e Séries - Volume  , Luís Lopes, QED TEXTE,
, Luís Lopes, QED TEXTE,  ;
;
 Manual de Fórmulas e Tabelas Matemáticas - Terceira edição, Coleção SCHAUM, Bookman,
Manual de Fórmulas e Tabelas Matemáticas - Terceira edição, Coleção SCHAUM, Bookman,  ;
;
 Fundamentos de Matemática Elementar, Volume
Fundamentos de Matemática Elementar, Volume 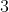 - Trigonometria, Atual Editora,
- Trigonometria, Atual Editora, 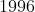 .
.
Gostará de ler também:
109-Seno e Cosseno de Ângulo Múltiplo
105-Versões Discretas da Transformada de Laplace e da Função Gama
029-Somatórios Trigonométricos
Gostará de ler também:
109-Seno e Cosseno de Ângulo Múltiplo
105-Versões Discretas da Transformada de Laplace e da Função Gama
029-Somatórios Trigonométricos
A TDL e Aplicações nas Equações de Recorrência ( do blog FATOS MATEMÁTICOS )



Olá Aloisio. Não consegui ler as equações acima. No seu computador elas aparecem normalmente?
ResponderExcluirSim, Paulo, normalmente, pelo menos no Firefox.
ExcluirEu passei a usar o Chrome depois que eu tive aquele problema no blog. Os outros publicados eu consigo ler. Acabei de ver o post de número 108 e as equações aparecem normalmente.
ExcluirCom o novo editor que eu uso, as vezes algumas fórmulas não funciona. O que eu faço é usar o Latex Online e colocar a equação na forma de imagem.
Tudo bem, vou ler com calma este seu post na forma que está.
Muito bom o post Aloisio. Usou apenas ferramentas elementares para obter as identidades trigonométricas e em consequência as TDL's de sin(na) e cos(na). Eu usei a identidade de Euler para obter as TDL's.
ResponderExcluirObrigado, Paulo.
ExcluirNa referência [1] da bibliografia as fórmulas para sen(na) e cos(na) são usadas sem demonstração para as provas dos somatórios mistos.
Para completar meus conhecimentos, eu adoraria ver seu processo para as TDL's das funções trigonométricas.
Abraços.
Oi, Teixeira!
ResponderExcluirHá muito tempo não "encaro" integrais e somatórios "escabrosos" mas me parece que são do teu gosto. Tomo a liberdade de lhe sugerir um livro: "Fisica Matemática de Butkov" Era (ou é) um livro-texto para os alunos de Física da USP.(720 páginas)(Eugene Butkov)
Veja o índice:
Vetores,matrizes e Cordenadas - Funções de uma variável complexa -Equações diferenciais lineares de segunda ordem - Séries de Fourier -Transformada de Laplace - Teoria das distribuições - Transformadas de Fourier -Equações diferenciais parciais -Funções especiais - Espaços de dimensão finita -Espaços de dimensão infinita - Funções de Green - Métodos variacionais -Ondas, radiação, espalhamento - Métodos de perturbação - Tensores
Espero que goste (caso não o conheça) abçs
Oi, Tavano!
ExcluirGosto muito de somatórios por serem o "buraco de minhoca" da matemática, se é que me entende.
Obrigado pela indicação do livro, eu não o conhecia. Gostei dos tópicos. Verei se encontro em algum sebo.
Valeu!