"O abandono da matemática traz dano a todo o conhecimento,
pois aquele que a ignora não pode conhecer as outras ciências
ou as coisas deste mundo."
O assunto do título é um dos mais interessantes em Teoria dos Números. Por certo, a maioria dos leitores aprendeu no ensino médio como somar, por exemplo, os números de pois aquele que a ignora não pode conhecer as outras ciências
ou as coisas deste mundo."
- Dado um inteiro positivo  , de quantas maneiras podemos representá-lo como somas de inteiros positivos consecutivos?
, de quantas maneiras podemos representá-lo como somas de inteiros positivos consecutivos?
- Como obter estas somas?
- Existem números que não podem ser representados como soma de inteiros positivos consecutivos?
Estas questões serão esclarecidas nas seções seguintes.
Seja uma progressão aritmética de razão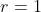 e primeiro termo
e primeiro termo 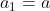 . Logo, seu enésimo termo é
. Logo, seu enésimo termo é 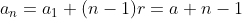 . Conforme a fórmula da soma dos
. Conforme a fórmula da soma dos  primeiros termos de uma
primeiros termos de uma 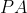 e fazendo desta soma um inteiro positivo
e fazendo desta soma um inteiro positivo  dado, temos
dado, temos
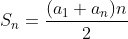
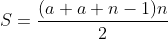
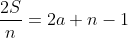 (1)
(1)
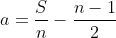 (2)
(2)
- Existem números que não podem ser representados como soma de inteiros positivos consecutivos?
Estas questões serão esclarecidas nas seções seguintes.
1.FÓRMULA GERAL DO PRIMEIRO TERMO
Seja uma progressão aritmética de razão
Reorganizando esta equação, obtemos
Concluímos então que, a primeira condição necessária para que  seja uma soma de inteiros consecutivos é que o número de termos
seja uma soma de inteiros consecutivos é que o número de termos  seja divisor do dobro da soma.
seja divisor do dobro da soma.
Reorganizando mais uma vez a nossa equação chegamos à
que é a fórmula do primeiro termo  . A segunda condição é que
. A segunda condição é que  seja inteiro e positivo e, para isto, devemos escolher convenientes divisores
seja inteiro e positivo e, para isto, devemos escolher convenientes divisores  de
de 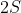 , conforme
, conforme  seja par ou ímpar.
seja par ou ímpar.
Observem que, em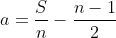 ,
,  é uma função decrescente de
é uma função decrescente de  . Desde que
. Desde que 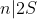 , ao colocarmos de modo crescente estes divisores
, ao colocarmos de modo crescente estes divisores  na fórmula acima,
na fórmula acima,  reduzirá o seu valor, se anulará ( o que não queremos ) e se tornará negativo ( o que não queremos ). Mas, podemos obter uma cota real superior de
reduzirá o seu valor, se anulará ( o que não queremos ) e se tornará negativo ( o que não queremos ). Mas, podemos obter uma cota real superior de  se considerarmos a equação em
se considerarmos a equação em

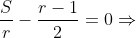
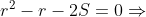
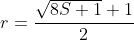 (3)
(3)
Logo os divisores  de
de 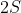 tais que
tais que 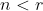 nos garante que o primeiro termo seja
nos garante que o primeiro termo seja 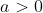 . Devemos então analisar estes divisores contidos no intervalo aberto
. Devemos então analisar estes divisores contidos no intervalo aberto 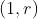 e verificar quais deles deixa o primeiro termo inteiro na fórmula
e verificar quais deles deixa o primeiro termo inteiro na fórmula 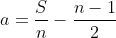 .
.
Por intermédio das equações (1) , (2) e (3) estudaremos todos os casos de representações de um número natural como soma de números positivos consecutivos .
Observem que, em
Por intermédio das equações (1) , (2) e (3) estudaremos todos os casos de representações de um número natural como soma de números positivos consecutivos .
2.POTÊNCIAS DE DOIS
Se 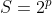 , com
, com 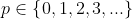 , então não pode ser representado como somas de inteiros positivos consecutivos.
, então não pode ser representado como somas de inteiros positivos consecutivos.
Demonstração. O número 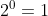 não pode ter a representação em questão por razões óbvias. Para
não pode ter a representação em questão por razões óbvias. Para 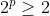 , vejamos.
, vejamos.
Se  for uma potência de dois, ou seja, se
for uma potência de dois, ou seja, se 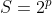 , com
, com  natural maior que
natural maior que  , então os divisores que interessam de
, então os divisores que interessam de 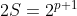 são da forma
são da forma 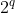 , com
, com 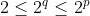 ( descartamos o divisor
( descartamos o divisor 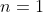 tendo em vista que, se este número é igual ao número de termos consecutivos, então tem que ser maior que um ) . Inserindo na fórmula
tendo em vista que, se este número é igual ao número de termos consecutivos, então tem que ser maior que um ) . Inserindo na fórmula 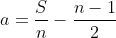 , temos
, temos
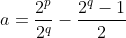
Demonstração. Conforme vimos, pela equação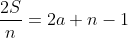 , o número de termos
, o número de termos  tem que ser divisor do dobro da soma. Ora, sendo
tem que ser divisor do dobro da soma. Ora, sendo  primo ímpar, os únicos divisores de
primo ímpar, os únicos divisores de 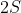 são
são  ,
,  ,
,  e
e 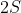 . Veremos agora cada divisor no cálculo do primeiro termo
. Veremos agora cada divisor no cálculo do primeiro termo 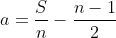 .
.
Para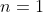 não consideramos pois não se pode falar de soma consecutiva com apenas um termo;
não consideramos pois não se pode falar de soma consecutiva com apenas um termo;
Para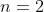 , temos
, temos 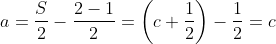 , onde
, onde  é um inteiro positivo
é um inteiro positivo
Para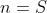 , temos
, temos 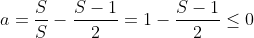 , pois
, pois  é um primo ímpar;
é um primo ímpar;
Para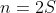 , temos
, temos 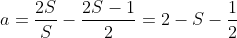 que não é inteiro e nem positivo.
que não é inteiro e nem positivo.
Concluímos então que o único caso em que o primeiro termo é um inteiro positivo é quando o número de termos é
é um inteiro positivo é quando o número de termos é 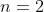 sendo esta a única forma em que o primo ímpar
sendo esta a única forma em que o primo ímpar  pode ser representado como soma de números positivos consecutivos.
pode ser representado como soma de números positivos consecutivos.
Exemplo. Colocar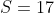 como soma de inteiros positivos consecutivos.
como soma de inteiros positivos consecutivos.
Pegamos então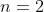 que é divisor do dobro da soma
que é divisor do dobro da soma 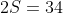 . Calculando o primeiro termo com nossa fórmula
. Calculando o primeiro termo com nossa fórmula 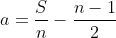 , temos
, temos 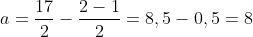 . Assim
. Assim 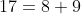 .
.
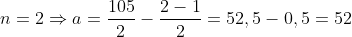 e
e
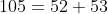
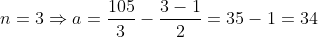 e
e
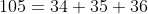
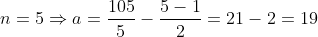 e
e
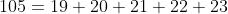
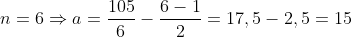 e
e
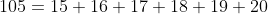
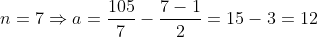 e
e
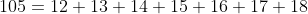
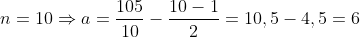
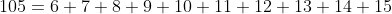 e
e
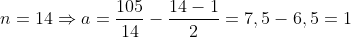 e
e
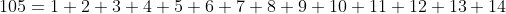
Observem que se  então
então 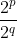 é inteiro mas
é inteiro mas 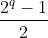 não é. Logo, neste caso,
não é. Logo, neste caso,  não é inteiro.
não é inteiro.
E se 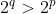 , então, tendo em vista que, no mínimo
, então, tendo em vista que, no mínimo 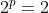 , temos
, temos 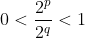 e
e 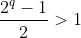 . Logo
. Logo  também não é inteiro por ser fracionário e/ou negativo.
também não é inteiro por ser fracionário e/ou negativo.
3.NÚMEROS PRIMOS
Se  for primo ímpar, então tem uma única representação como somas de inteiros positivos consecutivos.
for primo ímpar, então tem uma única representação como somas de inteiros positivos consecutivos.
Demonstração. Conforme vimos, pela equação
Para
Para
Para
Para
Concluímos então que o único caso em que o primeiro termo
Exemplo. Colocar
Pegamos então
4.NÚMEROS ÍMPARES
Excetuando-se
os números primos, todo número ímpar tem, no mínimo, duas formas de
representação como soma de números inteiros consecutivos.
Demonstração. Seja 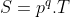 um número ímpar qualquer, com
um número ímpar qualquer, com  primo ímpar e
primo ímpar e 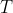 é o produto de potências de primos ímpares maiores que
é o produto de potências de primos ímpares maiores que  . Considere o divisor
. Considere o divisor 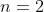 de
de 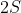 , número de termos da soma
, número de termos da soma  conforme a equação já vista
conforme a equação já vista 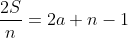 .
.
Para 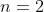 , temos
, temos 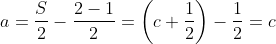 , onde
, onde  é um inteiro positivo.
é um inteiro positivo.
Logo,
qualquer número ímpar, composto ou primo, possui esta forma trivial de
representação como soma dos números positivos consecutivos 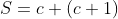 . Exemplos:
. Exemplos:  e
e 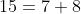 .
.
Vejamos agora que, ao contrário dos números primos, para um número ímpar composto esta forma de representação não é única.
De fato, pois para o número de termos 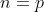 , temos como primeiro termo
, temos como primeiro termo 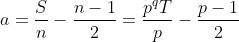 que é inteiro positivo porque no mínimo
que é inteiro positivo porque no mínimo 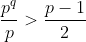 , para
, para 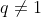 .
.
Para as outras formas de somas, os divisores de 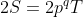 necessitam estar enquadrados no intervalo
necessitam estar enquadrados no intervalo 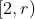 , sendo
, sendo  a cota real superior.
a cota real superior.
Exemplo. Colocar 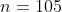 como somas de inteiros positivos consecutivos.
como somas de inteiros positivos consecutivos.
A cota real superior é 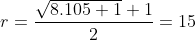 . Assim os números
. Assim os números  de termos das somas são divisores de
de termos das somas são divisores de 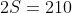 maiores que
maiores que  e menores que
e menores que 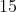 , ou seja,
, ou seja, 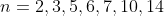 .
.
Calculando o primeiro termo de cada soma com a fórmula 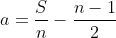 , temos
, temos
TEOREMA DE SEBÁ
Se um natural ímpar só puder ser expresso como
soma de dois naturais consecutivos, então, esse natural é um primo.
Este teorema é justificado nas seções 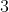 e
e 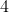 .
.
5.NÚMEROS PARES
Excetuando-se as potências de dois, alguns números pares podem ser
representados por uma ou mais somas de no mínimo três inteiros positivos
consecutivos.
Demonstração. Observem de imediato que, se  é par, então em
é par, então em 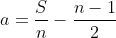 , temos que o número de termos
, temos que o número de termos  (divisor de
(divisor de 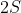 ) é obrigatório ser ímpar, pois é a única forma de
) é obrigatório ser ímpar, pois é a única forma de  ser inteiro.
ser inteiro.
Logo, para calcular os primeiros termos das somas de 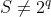 , temos que analisar apenas os divisores
, temos que analisar apenas os divisores  ímpares do número par
ímpares do número par  tais que
tais que 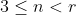 .
.
Exemplo. O primeiro par que não é potência de dois é 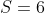 . A cota superior real é
. A cota superior real é 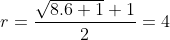 . Os divisores ímpares de
. Os divisores ímpares de 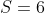 tais que
tais que 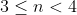 é unicamente
é unicamente 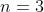 .
.
Calculando o primeiro termo 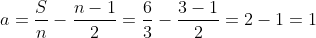 . Assim
. Assim 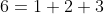 .
.
Exercício. Calcular todas as formas de representação de 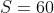 como soma de números positivos consecutivos.
como soma de números positivos consecutivos.
_*_
Referência na net:
http://gazeta.spm.pt/getArtigo?gid=151
Imagem: http://www.puzzleclopedia.com/division-exacta/



Brilhante esse artigo!!!
ResponderExcluirSempre procurei encontrar um algoritmo para determinar de maneira fácil se um número é primo e creio que este artigo me ajudou bastante.
Já tenho alguns macetes para determinar se um número é primo ou não tais como:
Dado um número n natural:
1) Testar se n = 2. Se for então é primo.
2) Caso contrário, testar se n é par. Se for então não é primo.
3) Caso contrário, testar se o resto de (n+1)/6 = 0 ou se o resto de (n-1)/6 = 0. Caso não seja 0 em nenhuma das duas divisões, então não é primo.
4) Caso contrário, testar se n é divisível por algum número ímpar entre 3 e a raiz quadrada de n. Caso seja, então não é primo.
5) Caso contrário, então é primo.
Como veem, tenho esses macetes em meu algoritmo de checagem da primalidade dos números inteiros.
Caso alguém tenha mais alguma dica para acrescentar nessa série de condições, ficarei muito agradecido.
Agora verificarei o quão rápido pode ser um algoritmo para determinar a primalidade de um número inteiro baseando-me no artigo exposto.
Obrigado.
Oi, Labrego e Roger!
ResponderExcluirEssa é a grande vantagem da fácil divulgação atual de artigos matemáticos: o quase automático intercâmbio de ideias, o que permite uma mútua ajuda aos pesquisadores.
Os testes de primalidade são uma veia de pesquisa muito promissora pois esta classe de números ainda é bastante resistente no desvendar de sua enigmática natureza, tanto que, quem conseguir, registrará o seu nome na eternidade.
Obrigado pela visita e sucesso nas suas pesquisas!
Este comentário foi removido pelo autor.
ResponderExcluirPara o caso 5, existe outra possibilidade:
ResponderExcluir"n" pode ser algum divisor de 2S, par, desde que seja o dobro do valor de algum divisor de S que não seja, também, divisor de S.
Exemplo:
S = 100
n = 5
n = 8
No caso de n = 25 ; n = 200 ; n = 40 - incluiriam-se os inteiros negativos.
Abraços, conteúdo esplendido!