"Qualquer um pode ser um matemático de primeira sem habilidade para fazer cálculos. E é possível ter um grande poder de cálculo sem ter a menor ideia do que é a Matemática."
Georg Novallis
Os matemáticos costumam inventar artifícios variados com o intuito de resolver problemas complexos ou até mesmo impossíveis por métodos tradicionais. Por exemplo, dividir um ângulo dado em três partes iguais apenas com régua não graduada e compasso é impossível mas não a partir de curvas especiais. Uma delas é a curva de Hípias que não só resolve a questão da trissecção angular como também o da quadratura do círculo. A quadratura consiste em encontrar com os instrumentos euclidianos ( régua e compasso) o lado de um quadrado de mesma mesma área que um círculo de raio conhecido.
A curva de Hípias, curva exótica mais antiga conhecida, foi criada pelo grego Hípias de Elis
Definição
Uma curva diz-se mecânica quando seus pontos são gerados pela interseção de figuras geométricas em movimento. É o caso da curva de Hípias.
Considere o quadrado 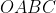 a seguir. A curva
a seguir. A curva 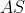 é a trissectriz de Hípias. Observe que, em uma mesma vertical, as ordenadas dos pontos desta curva são menores que as ordenadas dos pontos do quarto de círculo
é a trissectriz de Hípias. Observe que, em uma mesma vertical, as ordenadas dos pontos desta curva são menores que as ordenadas dos pontos do quarto de círculo  . Realmente uma curva estranha. Veremos agora sua lei de formação.
. Realmente uma curva estranha. Veremos agora sua lei de formação.
Considere os seguintes movimentos. A reta  move-se em movimento uniforme e vertical até coincidir com a reta
move-se em movimento uniforme e vertical até coincidir com a reta 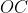 . No mesmo tempo que
. No mesmo tempo que  inicia seu movimento, a reta
inicia seu movimento, a reta 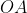 gira uniformemente e em sentido horário em torno do ponto
gira uniformemente e em sentido horário em torno do ponto 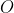 até coincidir também com a reta
até coincidir também com a reta 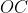 chegando ao mesmo tempo que a reta
chegando ao mesmo tempo que a reta  no seu movimento vertical.
no seu movimento vertical.
Em um dado momento, seja ![A1B1 [;A1B1;]](http://thewe.net/tex/A1B1) a posição da reta
a posição da reta  e
e 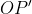 a posição da reta
a posição da reta 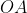 . O ponto
. O ponto  é a intersecção de
é a intersecção de ![A1B1 [;A1B1;]](http://thewe.net/tex/A1B1) e
e 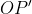 . O lugar descrito pelo ponto
. O lugar descrito pelo ponto  considerando todas as intersecções possíveis das retas
considerando todas as intersecções possíveis das retas  e
e 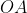 durante seus movimentos é a curva
durante seus movimentos é a curva 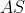 , a curva de Hípias.
, a curva de Hípias.
Trissecção
A mais importante propriedade da curva de Hípias é a proporcionalidade direta do segmento 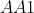 com o ângulo
com o ângulo 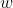 ou a proporcionalidade direta do segmento
ou a proporcionalidade direta do segmento 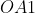 com o ângulo
com o ângulo 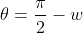 . É o que permite a trisseção.
. É o que permite a trisseção.
Teorema. O espaço vertical 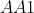 percorrido pelo segmento
percorrido pelo segmento ![A1B1 [;A1B1;]](http://thewe.net/tex/A1B1) é diretamente proporcional ao ângulo
é diretamente proporcional ao ângulo 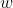 formado pelo segmento
formado pelo segmento 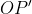 e o eixo
e o eixo 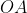 .
.
Demonstração. O movimento do segmento 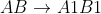 e do segmento
e do segmento 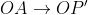 são uniformes, por definição. Logo, podemos fazer
são uniformes, por definição. Logo, podemos fazer 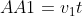 e
e 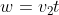 , onde
, onde 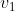 é a velocidade linear de
é a velocidade linear de  e
e 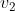 a velocidade angular de
a velocidade angular de 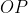 . Assim,
. Assim,
caracterizando a proporção direta do espaço linear percorrido 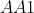 com do espaço angular percorrido
com do espaço angular percorrido 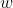 .
.
Consequentemente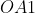 é diretamente proporcional a
é diretamente proporcional a 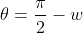 . É esta segunda visão de proporcionalidade que normalmente é utilizado na trissecção. Passaremos a descrever o processo da mesma. Contemplem o diagrama.
. É esta segunda visão de proporcionalidade que normalmente é utilizado na trissecção. Passaremos a descrever o processo da mesma. Contemplem o diagrama.
Consequentemente
Começamos dividindo o segmento 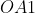 nas partes iguais
nas partes iguais 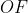 ,
, 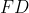 e
e 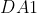 . Sejam
. Sejam  ,
, 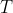 e
e 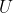 os pontos da curva de Hípias que interceptam os segmentos horizontais
os pontos da curva de Hípias que interceptam os segmentos horizontais ![A1B1 [;A1B1;]](http://thewe.net/tex/A1B1) ,
, 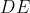 e
e 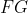 , respectivamente. Assim, os segmentos
, respectivamente. Assim, os segmentos 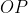 ,
, 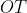 e
e 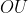 dividem o ângulo hachurado de vértice
dividem o ângulo hachurado de vértice 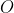 em três partes idênticas.
em três partes idênticas.
Da mesma forma, de dividíssemos o segmento 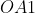 em
em  partes iguais, então se dividiria o ângulo hachurado em
partes iguais, então se dividiria o ângulo hachurado em  partes iguais, ou seja, Hípias tinha conseguido algo muito além do que uma trissecção angular, que era um problema em volga e importante da sua época.
partes iguais, ou seja, Hípias tinha conseguido algo muito além do que uma trissecção angular, que era um problema em volga e importante da sua época.
Equação Cartesiana e Polar
Vimos que 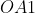 é diretamente proporcional ao ângulo
é diretamente proporcional ao ângulo  ou vice-versa. Tendo em vista que
ou vice-versa. Tendo em vista que 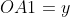 , temos
, temos
Para achar o valor da constante  atribuímos
atribuímos 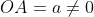 e verificamos que quando
e verificamos que quando 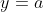 então
então 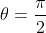 . Logo,
. Logo, 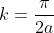 e
e
Mas vejam que 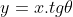 . Assim, a equação cartesiana da curva de Hípias é dado na forma implícita
. Assim, a equação cartesiana da curva de Hípias é dado na forma implícita
Para a equação polar, usaremos o raio da curva 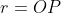 ( não confundir com o raio do quarto de círculo
( não confundir com o raio do quarto de círculo  que é
que é 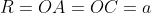 ) e o ângulo
) e o ângulo  . Sabemos que
. Sabemos que 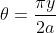 . Fazendo
. Fazendo 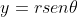 e substituindo chegamos a equação polar da curva de Hípias:
e substituindo chegamos a equação polar da curva de Hípias:
Quadratura

Fazer a quadratura do círculo com régua e compasso não é possível porque o número
Da equação polar
Logo, 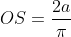
Interessante observar que 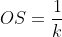 , onde
, onde  é a constante de proporcionalidade direta de
é a constante de proporcionalidade direta de  com o segmento
com o segmento 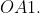
Para quadrar o círculo basta utilizar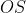 para construir um segmento do comprimento de
para construir um segmento do comprimento de  que é
que é 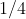 de circunferência de raio
de circunferência de raio 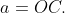 Então, um retângulo de medidas
Então, um retângulo de medidas 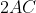 e
e 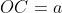 tem a mesma área que um círculo de raio
tem a mesma área que um círculo de raio 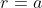 . Para finalizar constrói-se facilmente um quadrado com área igual a este retângulo.
. Para finalizar constrói-se facilmente um quadrado com área igual a este retângulo.
Para quadrar o círculo basta utilizar
Natureza Oculta da Curva de Hípias
A equação cartesiana da curva de Hípias 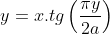 é implícita mas sua inversa não é. Trocando o
é implícita mas sua inversa não é. Trocando o  pelo
pelo  e vice-versa, temos:
e vice-versa, temos:
Assim fica bem mais simples fazer o gráfico com esta equação. Fazendo
Se a curva de Hípias, além da trissecção angular e da quadratura do círculo também resolvesse a questão da duplicação do cubo, então seria a curva mais genial já descoberta pois solucionaria todos os três problemas gregos famosos da antiguidade.
Referência Bibliográfica
Referência Bibliográfica
História de Matemática, Carl B. Boyer, Editora Edgard Blücher LTDA
Referência na NET:





Excelente post, com muitas informações relevantes e de forma concisa. Parabéns pela postagem e pelo retorno ao blog.
ResponderExcluirCom exceção da reta e do círculo, a curva de Hípias é a mais antiga da História da Matemática. Ainda não tentei mais fiquei curioso para saber a equação paramétrica desta curva. Obrigado!
Excluir