A equação diofantina linear 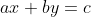 ou não tem nenhuma solução inteira ou possui infinitas soluções inteiras. Isto decorre do fato de que, se houver soluções inteiras, então
ou não tem nenhuma solução inteira ou possui infinitas soluções inteiras. Isto decorre do fato de que, se houver soluções inteiras, então  divide
divide 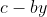 e
e  divide
divide 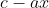 . E nem sempre isto é possível.
. E nem sempre isto é possível.
Já no artigo 019 provei que se 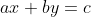 admitir uma solução
admitir uma solução 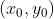 , então para todo
, então para todo 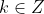 , as outras soluções
, as outras soluções 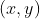 terão o formato
terão o formato
O par 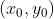 é chamado de solução inicial e pode ser achada pelo algoritmo de Euclides, um método essencialmente aritmético e, por vezes, trabalhoso ( ver artigos 017 e 019.)
é chamado de solução inicial e pode ser achada pelo algoritmo de Euclides, um método essencialmente aritmético e, por vezes, trabalhoso ( ver artigos 017 e 019.)
Mas, ainda no post 019, expus alguns atalhos para a solução inicial 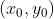 . No entanto, dependem da sorte dos coeficientes
. No entanto, dependem da sorte dos coeficientes  ,
,  e
e  . Seja, por exemplo, resolver
. Seja, por exemplo, resolver 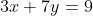 . Logo de cara vemos que
. Logo de cara vemos que 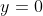 e
e 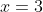 é uma solução inicial. Assim, as outras soluções são
é uma solução inicial. Assim, as outras soluções são 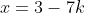 e
e 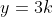 , com
, com 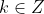 . Mas esta facilidade não temos para a equação
. Mas esta facilidade não temos para a equação 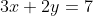 que tem soluções inteiras porque
que tem soluções inteiras porque 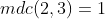 e divide
e divide 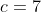 . Neste caso é empregado o algoritmo de Euclides... ou o método algébrico que sugiro no presente artigo e no qual explanarei a seguir.
. Neste caso é empregado o algoritmo de Euclides... ou o método algébrico que sugiro no presente artigo e no qual explanarei a seguir.
Existe uma maneira de fatorar 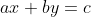 , mas da forma que se apresenta é impossível. É necessário uma fissão de variáveis. Conseguido a fatoração, podemos utilizar o método dos divisores complementares utilizado para resolver a equação
, mas da forma que se apresenta é impossível. É necessário uma fissão de variáveis. Conseguido a fatoração, podemos utilizar o método dos divisores complementares utilizado para resolver a equação 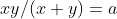 , conforme visto no artigo anterior.
, conforme visto no artigo anterior.
Seja a equação
Seja a equação
Dividindo ambos os membros pelo coeficiente  ,
,
Somando ambos os membros por 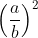 ,
,
Agora, fazendo 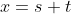 e
e 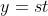 , com
, com  e
e 
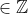 , temos
, temos
E passamos para a conhecida fatoração do trinômio em  do primeiro membro
do primeiro membro
Aqui, podemos chamar 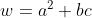 . Então
. Então 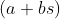 e
e 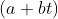 são divisores inteiros complementares de
são divisores inteiros complementares de 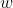 . Chamando estes divisores de
. Chamando estes divisores de 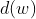 e
e 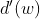 , onde
, onde 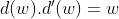 , temos
, temos 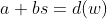 e
e 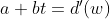 , de forma que
, de forma que
Exemplo. Achar uma solução inicial para a EDL 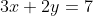 .
.
Temos então 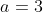 ,
, 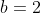 e
e 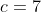 , com
, com 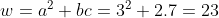
Os divisores inteiros de 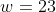 são
são 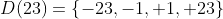
Pegando os dois primeiros complementares, temos
Logo, uma solução inicial para a equação 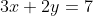 é
é 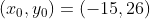 .
.
E as outras soluções são geradas por 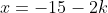 e
e 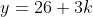 , com
, com 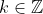 .
.


muito bom!!!!
ResponderExcluirObrigado, professor Rubens Sucupira!
ExcluirOi, Teixeira! A equação-exemplo acho que é 3x+2y=7 (2y não 2x)
ResponderExcluir"Fazendo x=s+t e y=st com s e t inteiros" Posto que isso nem sempre é possível, não sei qual a consequência dessa transformação, penso que talvez ela vá esconder alguns pares de solução, mas como as soluções são infinitas e se busca só uma inicial talvez sempre haja "s" e "t" inteiros pelo menos para um par (x;y).
Parabéns pela coragem de mexer em algo tão clássico, e mediante um golpe genial ter obtido uma nova solução para algo "imexível". Abçs.
Oi, amigo Tavano!
ExcluirValeu a correção, passou-me em branco. Já fiz as alterações.
Sobre sua observação e como "s" e "t" são dados em forma fracionária, com denominador "b", de repente nem seja necessário que estas duas variáveis sejam inteiras, desde que x=s+t e y=st sejam inteiros. Mas ainda não cheguei a testar isso.
Obrigado mais uma vez e matemática é isso aí, sempre com caminhos ocultos e rica em possibilidades. Abçs.
Por que esta parte final 2 + 2.1?
ResponderExcluir