A presente postagem é um trabalho para a Faculdade de Matemática
(FAMAT) da Universidade Federal de Uberlândia (UFU) na disciplina Informática e
Ensino. O professor Jocelino Sato propôs o seguinte.
"O assunto deste trabalho é o
software GeoGebra e constituirá de um material escrito
contendo um texto teórico sobre o
estudo de uma função (propriedades,
zeros, sinal, etc.),
junto com o desenvolvimento de pelo menos duas construções, fazendo uso
do GeoGebra,
que possibilitem obter as ilustrações (figuras) presentes no texto e
animações, mediante o
uso de parâmetros de animações (seletores), de propriedades vistas no
estudo teórico.
Todo material escrito será produzido fazendo uso de editores de textos
apropriados, por
exemplo, o LyX, e do software Geogebra. Mas, o produto final será
entregue no formato
.html em um único arquivo, contendo
o desenvolvimento do assunto (texto teórico contendo
exemplos e ilustrações) e recursos (pelo menos dois Applets do Geogebra)
que forneçam interfaces gráficas passíveis de serem manipuladas pelos
usuário, instigando a curiosidade e
a descoberta dos conceitos matemáticos."
Estudaremos a função definida por
nos seguintes aspectos: domínio, período, imagem, amplitude,
intersecção com os eixos coordenados, sinal, intervalos de
crescimento e decrescimento, pontos de máximo e pontos de
mínimo. Ao final da análise, faremos dois gráficos.
A função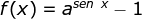 assume o mesmo
domínio e período de
assume o mesmo
domínio e período de 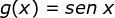 , ou
seja,
, ou
seja,  e
e  .
.
A imagem ou os valores que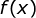 pode assumir vai
depender se
pode assumir vai
depender se 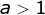 ou se
ou se 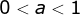 . Isto porque os
valores de
. Isto porque os
valores de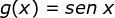 estão limitados no
intervalo
estão limitados no
intervalo 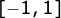 e caso
e caso 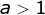 , temos que a imagem
de
, temos que a imagem
de 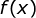 é o intervalo
é o intervalo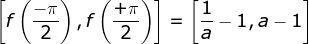 . Por outro lado,
se
. Por outro lado,
se 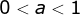 , temos a imagem no
intervalo
, temos a imagem no
intervalo 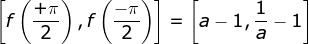 . Se a base
. Se a base 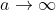 ou
ou 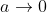 , os limites do intervalo da imagem são tais que
, os limites do intervalo da imagem são tais que 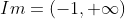 , em ambos os casos.
, em ambos os casos.
Defino como amplitude de uma função periódica limitada o módulo da diferença dos limites do intervalo de sua imagem. Assim, a amplitude de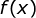 é
é 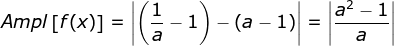 .
.
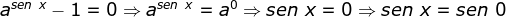
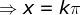 , com
, com 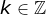
Da função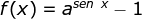 já sabemos todos os pontos tais que
já sabemos todos os pontos tais que 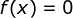 . Nos interessa agora o
intervalo onde
. Nos interessa agora o
intervalo onde 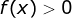 e o intervalo
onde
e o intervalo
onde 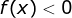 . Temos dois casos a
considerar relativo à base
. Temos dois casos a
considerar relativo à base 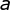 .
.
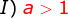 .
.
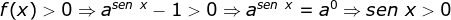
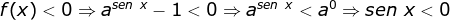

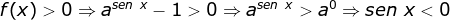
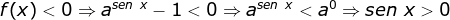
Domínio, período, imagem e
amplitude
A função
A imagem ou os valores que
Defino como amplitude de uma função periódica limitada o módulo da diferença dos limites do intervalo de sua imagem. Assim, a amplitude de
Intersecção com os eixo
coordenados
O gráfico da função definida por 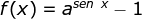 intersecta
simultaneamente o eixo
intersecta
simultaneamente o eixo 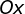 e
e 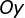 no ponto
no ponto 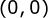 , pois
, pois 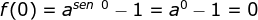 . Por
definição de função, o ponto
. Por
definição de função, o ponto  é único.
é único.
Acharemos agora todos os pontos do tipo  . Fazendo
. Fazendo 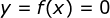 , temos
, temos
Logo, os pontos de intersecção do gráfico de 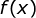 com o
eixo
com o
eixo 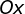 são da
forma
são da
forma 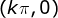 , com
, com 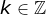 .
.
Sinal da função
Da função
Então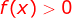 para
para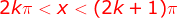
Então 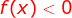 para
para 
.
Então 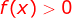 para
para 
Então 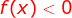 para
para 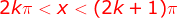
Intervalos de crescimento e
decrescimento
Calculemos a derivada de
Sendo
Novamente, temos dois casos a considerar.
Neste caso, o sinal de 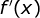 dependerá
exclusivamente do fator
dependerá
exclusivamente do fator 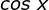 .
.
Então a função 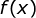 é crescente para
é crescente para 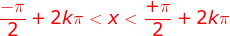
Então a função 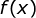 é decrescente
para
é decrescente
para 
Então a função 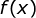 é crescente para
é crescente para 
Então a função 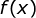 é decrescente para
é decrescente para 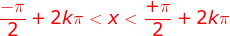
Pontos de máximo e pontos de
mínimos
Nos pontos de máximo e mínimo as derivadas são nulas.
Fazendo 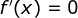 , temos
, temos
Analisando os intervalos de crescimento e decrescimento calculados na
seção anterior, concluímos que
se 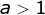 , temos pontos de máximo
para
, temos pontos de máximo
para 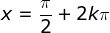 e pontos de mínimo
para
e pontos de mínimo
para 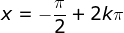 . Caso
. Caso 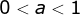 , temos pontos
máximos para
, temos pontos
máximos para 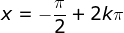 e pontos de mínimo
para
e pontos de mínimo
para 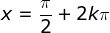 .
.
O gráfico
Coletando todos os dados calculados, estamos em condições de construir
um gráfico com recursos informativos e interativos de qualidade, utilizando uma poderosa ferramenta para estudos
matemáticos, o software gratuito GEOGEBRA (
https://www.geogebra.org/?lang=pt_BR).
Faremos dois gráficos. Um para 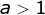 e outro
para
e outro
para 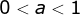 .
.
Caro leitor, use as barretas de rolagem acima e à esquerda do gráfico para alterar os dados do mesmo. Nestas ferramentas,  é a base da expressão
é a base da expressão 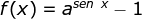 que define a função em estudo e
que define a função em estudo e é o parâmetro inteiro de periodicidade de
é o parâmetro inteiro de periodicidade de  , tendo em vista que
, tendo em vista que 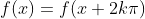 .
.

Nenhum comentário:
Postar um comentário