Da mesma forma define-se a diretiva (
(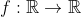 ) da função
) da função 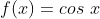 :
:
Observem os leitores que para 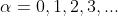 , a diretiva
, a diretiva  de
de 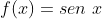 coincide com a definição de derivada
coincide com a definição de derivada  -ésima de
-ésima de 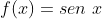 . De fato, pois
. De fato, pois
Notem, ainda que, para
Essa mesma propriedade da diretiva podemos verificar para a função
Do exposto, podemos concluir que, para
Mas, as diretivas  de
de 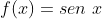 e
e 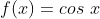 foram definidas para
foram definidas para  racional. O que significa então, em termos de derivada, por exemplo, a diretiva
racional. O que significa então, em termos de derivada, por exemplo, a diretiva 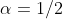 de
de 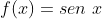 ? Em outras palavras, o que significa a derivada meiésina de
? Em outras palavras, o que significa a derivada meiésina de 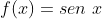 ?
?
Condizente com a estrutura das derivadas sucessivas, onde derivar  vezes uma função é calcular a derivada
vezes uma função é calcular a derivada 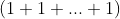 -ésima desta função ( dentro do parêntese tempos
-ésima desta função ( dentro do parêntese tempos  parcelas iguais a
parcelas iguais a  ), podemos ensaiar a seguinte definição de derivada meiésima:
), podemos ensaiar a seguinte definição de derivada meiésima:
Derivada meiésima de  é a operação que, aplicada duas vez em
é a operação que, aplicada duas vez em  , obtêm-se
, obtêm-se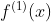 . Simbolicamente,
. Simbolicamente,
Vamos verificar se, com essa definição, a derivada meiésima de 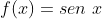 é coincidente com a diretiva
é coincidente com a diretiva 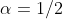 da mesma função. Vejamos, para
da mesma função. Vejamos, para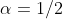 , temos
, temos
e
Suponha 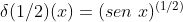 . Vamos então calcular o resultado de
. Vamos então calcular o resultado de
usando as fórmulas de diretiva para ver se chegamos a 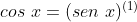 .
.
Assumindo que as propriedades 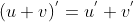 e
e 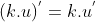 das derivadas normais também são válidas para as derivadas fracionárias, temos
das derivadas normais também são válidas para as derivadas fracionárias, temos
o que queríamos mostrar.
Dado  inteiro positivo e seguindo a mesmo lógica, podemos definir a derivada de "ordem"
inteiro positivo e seguindo a mesmo lógica, podemos definir a derivada de "ordem" 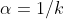 de uma função
de uma função  a operação que, aplicada
a operação que, aplicada  vezes em
vezes em  , obtêm-se
, obtêm-se 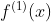 .
.
Fica como desafio aos leitores verificar se essa última definição é compatível com a diretiva 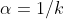 , de
, de 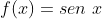 ou
ou 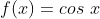 .
.
Conjectura: a correspondência (1) é válida para todo e qualquer  racional .
racional .



Seja bem-vindo de volta.
ResponderExcluira.Tavano
Oi, Teixeira. Esses assuntos sempre me fascinaram, lembrei-me que há uns quarenta anos eu estava pensando o que seria uma função de meia variável!!!
ResponderExcluirAproveitando sua ideia. Podemos supor que a derivada n-ésima de x^k é {k!/(n-k)!](x^(n-k)) isso daria para x°=1 que a derivada meio-ésima de 1 seria 1/sqrt(pix)
Loucura, kk
Oi, Tavano
ExcluirO Paulo Sérgio escreveu algo a respeito para potências.
Confira em http://fatosmatematicos.blogspot.com.br/2011/01/uma-breve-historia-do-calculo.html
Abraços
Desculpe, onde se lê (n-k)! e X^(n-k), leia-se (k-n)! e X^(k-n).
ResponderExcluir