Depois de uma longa ausência e agora na condição de estudante de graduação de matemática ( bacharelado ), volto com um interessante artigo sobre limite.
Considere dois polinômios 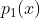 e
e 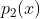 de mesmo grau
de mesmo grau 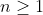 e em ambos o coeficiente do termo de maior grau é
e em ambos o coeficiente do termo de maior grau é  . Suponha que estes polinômios quando considerados como equações, ou seja,
. Suponha que estes polinômios quando considerados como equações, ou seja, 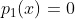 e
e 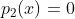 , possuam todas as suas raízes reais e que a soma destas raízes sejam respectivamente,
, possuam todas as suas raízes reais e que a soma destas raízes sejam respectivamente,
Então,
DEMONSTRAÇÃO
Aqui podemos utilizar o limite fundamental 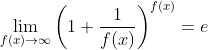 em cada fator do numerador e em cada fator do denominador desta expressão. Sejam
em cada fator do numerador e em cada fator do denominador desta expressão. Sejam  e
e 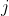 inteiros positivos.
inteiros positivos.
Identificamos que 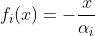 , com
, com 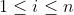 , relacionado aos fatores do numerador e que
, relacionado aos fatores do numerador e que 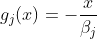 , com
, com 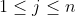 , relacionado aos fatores do denominador. Veja que
, relacionado aos fatores do denominador. Veja que
Logo,
Exemplo 1. Calcular 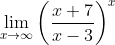 . Temos
. Temos  , com
, com 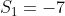 e
e 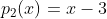 , com
, com 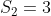 . Segue que
. Segue que 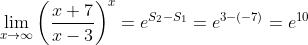
Exemplo 2. Calcular 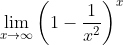 . Este limite é equivalente a
. Este limite é equivalente a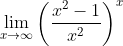 . O polinômio do numerador é
. O polinômio do numerador é 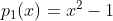 e o polinômio do denominador é
e o polinômio do denominador é 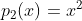 . Ambos possuem o mesmo grau e raízes reais cujas somas são
. Ambos possuem o mesmo grau e raízes reais cujas somas são 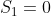 e
e 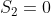 , respectivamente. Assim,
, respectivamente. Assim, 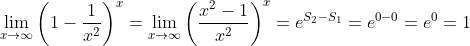
Exemplo 3. Calcular 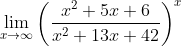 . Por intermédio do discriminante delta sabemos que as funções polinomiais
. Por intermédio do discriminante delta sabemos que as funções polinomiais 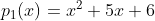 e
e 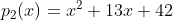 possuem zeros reais. Pelas relações de Girard encontramos que a soma destes zeros referente a cada polinômio é
possuem zeros reais. Pelas relações de Girard encontramos que a soma destes zeros referente a cada polinômio é 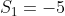 e
e 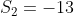 . Logo,
. Logo,
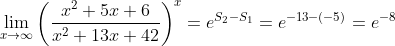
Exemplo 4. Sabendo que o conjunto solução da equação 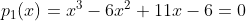 é
é 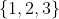 , calcule o limite
, calcule o limite 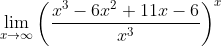 . Temos, de
. Temos, de 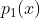 que
que 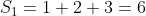 e
e 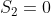 referente a
referente a 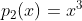 . Portanto,
. Portanto,
Pergunta aos leitores. O teorema também é válido para raízes complexas ?


Aloisio,
ResponderExcluirmandou muito bem com esse teorema e demonstração, nunca tinha visto algo do tipo!
Bom, através do seu teorema eu fui calcular alguns limites com raizes complexas, porem coloquei as assintotas no geogebra e vi que deu certo também com raízes complexas, só ainda n sei provar! Fica como exercício ;)
Abraço do seu amigo!
Tiago!
ExcluirAqui no blog também publico contribuições dos amigos. Caso tenha algo interessante, original ou não, pois o que importa é o aprendizado, sua versão da demonstração.
Valeu!
Muito bom o post Aloísio. Está de parabéns por mais esta contribuição a Matemática.
ResponderExcluirObrigado, Paulo!
ResponderExcluirVerei se consigo uma periodicidade confortável.
Abraços