Chamo de o enésimo número livre de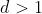 
ao enésimo inteiro positivo não-múltiplo de 
. Simbolizo por 
.
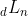A sequência dos números ímpares 
consiste nos números livres de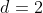 
. Seu termo geral é 
.
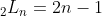A sequência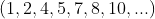 
representa os números livres de 
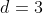. Qual a fórmula do termo genérico de 
?
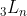Na sucessão 
temos os números livres de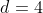 
. Como podemos calcular 
?
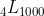Qual a fórmula do termo geral 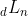dos números livres de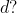 
Para responder a estas perguntas, precisamos conhecer ou lembrar da função colchete, onde, dado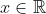 
, a mesma é definida como 
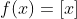= parte inteira de 
, se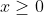 
. No caso de 
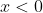, temos 
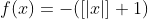. Só usaremos a primeira opção pois trabalharemos apenas com sucessão de números positivos. No entanto, segue-se exemplos gerais.
Duas operações envolvendo a função colchete que usarei neste artigo:
1) Dado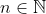 
e 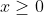, obviamente, 
;
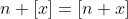2) Dados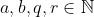 
, com 
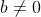e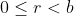 
e se temos 
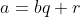, então é fácil verificar intuitivamente que 
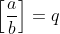, ou seja 
é a parte inteira da divisão de 
por 
.
LEMA. Na sequência definida por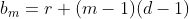 
, com 
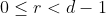, temos que não divide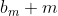 
.
Exemplo: se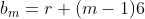 
, com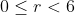 
, então 
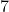não divide .
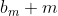Demonstração.
Ora, 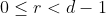implica em 
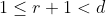, logo não pode dividir a soma .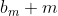
Para maior compreensão, usando o exemplo do lema com 
, ou seja, 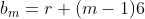, temos
E como 
, segue que 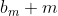não é múltiplo de .
TEOREMA. Se 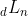representa o enésimo número livre de , então
Demonstração. Observe que em 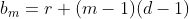, temos ( ver 2) ) 
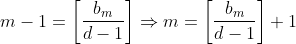. Assim,
Como vimos pelo LEMA demonstrado,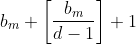 
nunca é múltiplo de .
O próximo passo, para conseguir 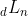, é ordenar 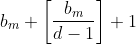, ou seja, colocar em função de 
.
Dado o inteiro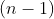 
, com 
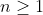, temos que qualquer elemento do conjunto 
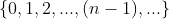quando dividido por 
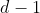, deixa resto 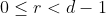. Assim, os elementos deste conjunto podem ser representados pela sequência de termo geral 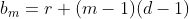. Podemos, então fazer, 
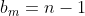, logo
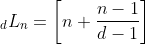( ver 1) )
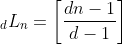
Desta forma,
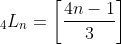
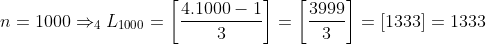
Desta forma,
Na sequência dos números ímpares , 
;
Nos números livres de 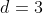, cujos primeiros termos são 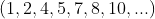, temos 
;
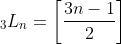Na sucessão dos números livres de 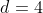, temos que o milésimo termo da sequência é calculado como se segue.
Nenhum comentário:
Postar um comentário