Considere o plano cartesiano a seguir. Nele locaremos pontos de coordenadas 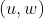 e
e 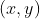 . No eixo horizontal estão as abcissas reais
. No eixo horizontal estão as abcissas reais 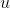 e
e  e no eixo vertical encontramos as ordenadas reais
e no eixo vertical encontramos as ordenadas reais 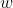 e
e  .
.
O ponto 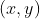 depende do ponto
depende do ponto 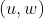 por intermédio da seguinte construção geométrica.
por intermédio da seguinte construção geométrica.
No retângulo de vértices 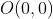 ,
, 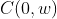 ,
, 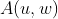 e
e 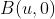 ( retângulo das coordenadas do ponto
( retângulo das coordenadas do ponto 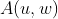 ) , traçamos a diagonal de extremidades
) , traçamos a diagonal de extremidades 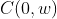 e
e 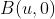 . Em seguida, traçamos o segmento
. Em seguida, traçamos o segmento 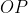 , que sai da origem
, que sai da origem 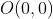 e é perpendicular à
e é perpendicular à  .
.
O ponto 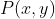 é o ponto de perpendicularismo ou intersecção entre
é o ponto de perpendicularismo ou intersecção entre 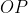 e
e  .
.
Tal plano cartesiano de coordenadas duplas e dependentes, conforme descrito, chamarei de plano WY.
Transformada WY da equação 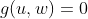 é a equação
é a equação 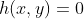 que esboça o lugar geométrico de todos os pontos
que esboça o lugar geométrico de todos os pontos 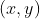 relacionados com os pontos
relacionados com os pontos 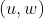 , conforme o plano WY.
, conforme o plano WY.
Para calcular a equação transformada 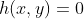 a partir da equação primitiva
a partir da equação primitiva 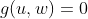 , é necessário relacionar as coordenadas do ponto
, é necessário relacionar as coordenadas do ponto 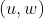 com as coordenadas do ponto
com as coordenadas do ponto 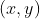 .
.
Tendo em vista que o triângulo retângulo 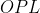 é semelhante aos triângulos retângulos
é semelhante aos triângulos retângulos 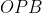 e
e 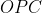 , temos as seguintes proporções.
, temos as seguintes proporções.
As igualdades 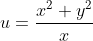 e
e 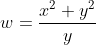 são as identidades de transformação WY.
são as identidades de transformação WY.
A seguir veremos exemplos de transformadas WY de equações da forma 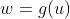 que definem funções, o que não se pode dizer sempre o mesmo das respectivas transformadas
que definem funções, o que não se pode dizer sempre o mesmo das respectivas transformadas 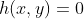 , pois as mesmas normalmente são em forma implícita e nem sempre representam funções.
, pois as mesmas normalmente são em forma implícita e nem sempre representam funções.
No plano WY, colocarei a curva da equação primitiva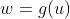 na cor vermelha e a curva da equação transformada
na cor vermelha e a curva da equação transformada 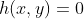 na cor azul.
na cor azul.
Usando as identidades de transformação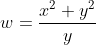 e
e 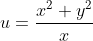 em
em 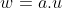 , obtemos
, obtemos
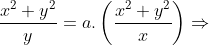
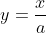
Logo, se 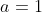 , temos
, temos 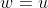 e
e 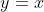 . Neste caso, como essas curvas são em um mesmo sistema de coordenadas cartesianas, ficamos com duas retas coincidentes de coeficientes
. Neste caso, como essas curvas são em um mesmo sistema de coordenadas cartesianas, ficamos com duas retas coincidentes de coeficientes 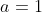 .
.

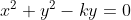
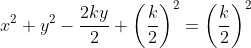
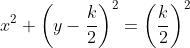
No plano WY, colocarei a curva da equação primitiva
Transformada de 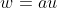 ( função afim,
( função afim, 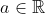 , com
, com 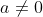 )
)
Usando as identidades de transformação
ou seja, uma reta com coeficiente inverso de 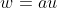
Transformada de 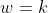 ( função constante,
( função constante,  e
e 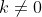 )
)
Substituindo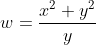 na equação
na equação 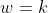 , temos
, temos
Assim, a transformada WY da equação 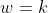 é a equação de um círculo de centro
é a equação de um círculo de centro 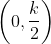 e raio
e raio 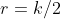 .
.
Transformada de 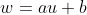 , com coeficientes reais e não nulos
, com coeficientes reais e não nulos
Se
Existem cinco entes geométricos notáveis no qual surgem cinco perguntas. Qual o valor de
A curva em azul é parecida com o folio de Descartes de equação
Transformada de 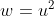
A curva resultante caracteriza todas as transformadas de equações do tipo 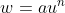 com
com 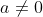 e
e  par, diferindo apenas no grau de abertura das curvas. Caso
par, diferindo apenas no grau de abertura das curvas. Caso  seja ímpar, os ramos esquerdos vermelho e azul das curvas se apresentariam no terceiro quadrante, com as respectivas concavidades invertidas.
seja ímpar, os ramos esquerdos vermelho e azul das curvas se apresentariam no terceiro quadrante, com as respectivas concavidades invertidas.
Transformada de 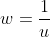
A curva é uma lemniscata inclinada nos quadrantes primeiro e terceiro. Lembrando que a lemniscata de Bernoulli, de equação 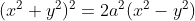 , é simétrica em relação ao eixo
, é simétrica em relação ao eixo 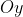 e
e 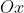 .
.
Gostará de ler também:
104 - As Ovais de Cassini e a Lemniscata de Bernoulli
107-Equação (y^2+x)^2=x
114 - Comportamento Gráfico de Certas Relações
116- Experências em 3D no Wolfran Alpha
118-Curva de Hípias
Referência na net:
http://pt.wikipedia.org/wiki/Folium_de_Descarteshttp://pt.wikipedia.org/wiki/Lemniscata_de_Bernoulli













Nenhum comentário:
Postar um comentário