e dele podemos extrair as regras gerais de derivação, como a regra da soma e a regra do produto de funções, etc, assim como as regras específicas, por exemplo, a derivada de uma potência  .
.
No entanto, podemos calcular as derivadas de 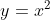 ,
, 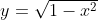 e
e 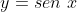 usando apenas matemática elementar. São exercícios interessantes de geometria analítica e plana.
usando apenas matemática elementar. São exercícios interessantes de geometria analítica e plana.
Derivada de 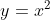
No caso de 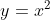 , se queremos encontrar a inclinação
, se queremos encontrar a inclinação  da reta tangente ao ponto
da reta tangente ao ponto 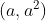 da parábola, primeiramente encontramos a equação da reta que passa pelo ponto
da parábola, primeiramente encontramos a equação da reta que passa pelo ponto 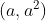 , ou seja,
, ou seja, 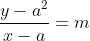 ou
ou 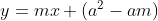 . Mas, pelo ponto
. Mas, pelo ponto 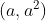 passam infinitas retas.
passam infinitas retas.
Para que a equação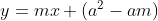 seja a da reta tangente que procuramos, é necessário que a igualdade
seja a da reta tangente que procuramos, é necessário que a igualdade 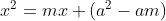 tenha uma única solução, tendo em vista que existe um único ponto de contato. Isto é um caso de discriminante delta nulo na equação equivalente
tenha uma única solução, tendo em vista que existe um único ponto de contato. Isto é um caso de discriminante delta nulo na equação equivalente 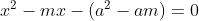 . Vejamos,
. Vejamos,
Para que a equação
Isto prova que 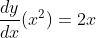 , pois o ponto
, pois o ponto 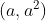 pode ser qualquer um da parábola ou
pode ser qualquer um da parábola ou 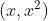 .
.
Sabemos, pela geometria plana que, se temos duas retas de inclinações 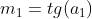 e
e 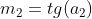 e se as mesmas são perpendiculares entre si, então
e se as mesmas são perpendiculares entre si, então 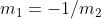 .
.
No diagrama, queremos achar a inclinação da reta tangente ao semicírculo no ponto . A inclinação do raio é
. A inclinação do raio é 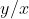 , logo, como o raio passando por
, logo, como o raio passando por  é perpendicular à tangente em
é perpendicular à tangente em  , temos que a inclinação da tangente ao semicírculo neste ponto é
, temos que a inclinação da tangente ao semicírculo neste ponto é 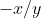 .
.
Como a equação do semicírculo é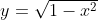 , decorre que
, decorre que
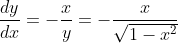
Derivada de 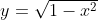
No diagrama, queremos achar a inclinação da reta tangente ao semicírculo no ponto
Como a equação do semicírculo é
Derivada de 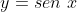
Considere o ponto  (vermelho) em movimento circular uniforme (
(vermelho) em movimento circular uniforme ( 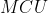 ), sentido anti-horário, com raio de trajetória
), sentido anti-horário, com raio de trajetória 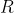 e espaço angular inicial zero, ou seja, quando
e espaço angular inicial zero, ou seja, quando 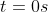 , temos
, temos 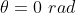 , medidos a partir do eixo horizontal, no primeiro quadrante e no sentido do movimento.
, medidos a partir do eixo horizontal, no primeiro quadrante e no sentido do movimento.
O tempo de uma volta completa é o período 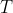 . Assim, a velocidade angular é
. Assim, a velocidade angular é 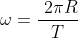 e o espaço angular é dado por
e o espaço angular é dado por 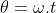 . O espaço e velocidade do ponto
. O espaço e velocidade do ponto  na própria trajetória são dados por
na própria trajetória são dados por 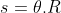 e
e 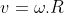 .
.
Seja agora o ponto  (azul) a projeção do ponto
(azul) a projeção do ponto  no eixo
no eixo 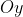 . Acompanhando o movimento do ponto vermelho, o ponto azul faz um movimento oscilatório "para cima" e "para baixo", cujos extremos de espaço são
. Acompanhando o movimento do ponto vermelho, o ponto azul faz um movimento oscilatório "para cima" e "para baixo", cujos extremos de espaço são 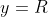 e
e 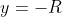 .
.
Nos interessa calcular as funções horárias do espaço  e velocidade
e velocidade 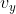 , do ponto azul.
, do ponto azul.
Pelo diagrama ,verifique que o espaço percorrido pelo ponto azul no eixo vertical é 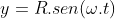 . Já
. Já 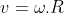 é o módulo do vetor velocidade do ponto vermelho na própria trajetória. Seja o vetor velocidade
é o módulo do vetor velocidade do ponto vermelho na própria trajetória. Seja o vetor velocidade 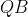 a projeção do vetor velocidade
a projeção do vetor velocidade 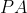 sobre o eixo
sobre o eixo 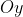 . Assim, pela relação entre os triângulos retângulos temos que
. Assim, pela relação entre os triângulos retângulos temos que 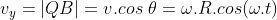 .
.
Ora, pelo Cálculo sabemos que, se 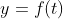 , então
, então 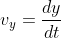 . Logo o que vimos foi uma prova cinemática de que
. Logo o que vimos foi uma prova cinemática de que 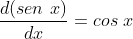 , para
, para 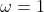 e
e 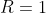 .
.
Para provar cinematicamente que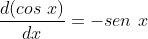 basta considerar o mesmo movimento circular de
basta considerar o mesmo movimento circular de  , mas com projeção no eixo
, mas com projeção no eixo 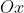 .
.
Para provar cinematicamente que





Muito legal.
ResponderExcluirEsse blog é excelente. Mas algumas imagens custumam ficar ausente .Alguem tem alguma ideia de como resolver o problema??
ResponderExcluirEste topico,por exemplo, eu nao consigo visualizar as imagens e as expressoes matematicas (eu acho) :http://elementosdeteixeira.blogspot.com.br/2012/04/geometria-e-gravidade.html
O que eu faço?
Caro visitante, pretendo corrigir os artigos anteriores, mas levará um tempo.
ResponderExcluirObrigado pela visita.
Ah, tudo bem Aloisio Teixeira. Pensei que estivesse aconteecendo só comigo.
ResponderExcluir