Eu queria colocar o título como "Método Alternativo para a Demonstração da Fórmula de Bhaskara" mas resolvi escrever um pouco sobre as equações cúbicas.
Vamos trabalhar com coeficientes reais na resolução de todas as equações propostas (
Seja a equação do 2º grau
e compare com 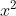
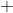
 .x +
.x +  = 0
= 0
A identidade em 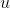 e
e  é válida para quaisquer que sejam estes valores.
é válida para quaisquer que sejam estes valores.
Já a equação em  é válida para valores específicos desta incógnita.
é válida para valores específicos desta incógnita.
No entanto, fazendo
podemos achar as raízes  utilizando a identidade e filtrando apenas os valores
utilizando a identidade e filtrando apenas os valores 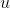 e
e  que satisfaçam o sistema acima. E isso não é tão difícil porque de ( 2 ) tiramos
que satisfaçam o sistema acima. E isso não é tão difícil porque de ( 2 ) tiramos  e substituindo em ( 3 ), temos:
e substituindo em ( 3 ), temos:
e de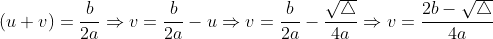
De forma que , 
A mesma estratégia podemos usar para resolver a equação cúbica incompleta 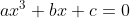 . Agora utilizaremos a identidade
. Agora utilizaremos a identidade
para montamos o sistema
De ( 2 ), temos 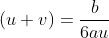 e inserindo em ( 3 ),
e inserindo em ( 3 ),  e isto nada mais é do que uma equação quadrática em
e isto nada mais é do que uma equação quadrática em  do qual achamos
do qual achamos 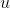 e de ( 2 ) achamos
e de ( 2 ) achamos  . Na sequência,
. Na sequência, 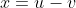 , refletindo o método de Cardano ( 1501-1576 ) para resolução de equações cúbicas.
, refletindo o método de Cardano ( 1501-1576 ) para resolução de equações cúbicas.
REFERÊNCIA BIBLIOGRÁFICA
História da Matemática de Carl.B.Boyer, Editora Edgard Blücher, 1994.
REFERÊNCIA BIBLIOGRÁFICA
História da Matemática de Carl.B.Boyer, Editora Edgard Blücher, 1994.


Nenhum comentário:
Postar um comentário