Para isso, apenas memorize a seguinte tabela numérica.
Observe que os números da coluna A são os números naturais de  a
a 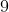 .
.
Na coluna B temos os cubos dos números da primeira coluna.
E na coluna C consta os últimos dígitos dos números da coluna B.
Primeiro exemplo. Qual a raiz cúbica de 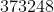 ?
?
Passo 1: Separa-se o número de três em três dígitos da direita para a esquerda  :
: 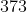 .
.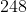 .
.
Passo2: Enquadra-se a primeira parte desta separação, que é 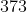 , entre os números da coluna do B. Assim, verifique que
, entre os números da coluna do B. Assim, verifique que 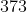 está entre
está entre 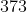 e
e 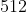 .
.
Passo3: Pegue o menor número do enquadramento (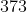 ) e verifique a sua correspondência com a coluna A. Portanto, encontramos o
) e verifique a sua correspondência com a coluna A. Portanto, encontramos o 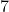 , o primeiro dígito da raiz cúbica procurada.
, o primeiro dígito da raiz cúbica procurada.
Passo 4: Pegue o último dígito de 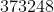 , que é
, que é 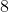 . Localize-o (
. Localize-o ( 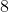 ) na coluna C e verifique sua correspondência com a coluna esquerda. Veja, então, que
) na coluna C e verifique sua correspondência com a coluna esquerda. Veja, então, que 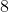 na coluna C corresponde com
na coluna C corresponde com  na coluna A. Assim,
na coluna A. Assim,  é o segundo dígito da raiz cúbica procurada.
é o segundo dígito da raiz cúbica procurada.
Resposta  a raiz cúbica de
a raiz cúbica de 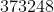 é
é 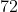 .
.
Segundo exemplo. Qual a raiz cúbica de 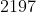 ?
?
Passo1: .
.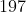 .
.
Passo2: Na coluna do B, está entre
está entre  e
e 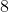 .
.
Passo3: O menor número do enquadramento ( ) corresponde a
) corresponde a  na coluna A. Portanto
na coluna A. Portanto  é o primeiro dígito procurado.
é o primeiro dígito procurado.
Passo4: O último dígito de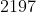 é
é 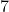 . Sua localização (
. Sua localização ( 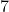 ) na coluna C corresponde à
) na coluna C corresponde à 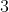 na coluna A. Portanto,
na coluna A. Portanto, 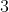 é o segundo dígito procurado.
é o segundo dígito procurado.
Resposta a raiz cúbica de
a raiz cúbica de 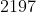 é
é 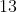 .
.
Porque este processo funciona? A resposta está nas RELAÇÕES DE CONGRUÊNCIA.
O conceito e a notação de congruência ( ) inventada pelo grande matemático alemão Carl Friedrich Gauss
) inventada pelo grande matemático alemão Carl Friedrich Gauss 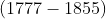 são explanados a seguir.
são explanados a seguir.
Dados ,
, 
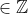 e
e 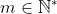 :
:
Diz-se que é congruente a
é congruente a  módulo
módulo  [ anota-se
[ anota-se 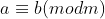 ] quando
] quando  e
e  , divididos por
, divididos por  , deixam o mesmo resto
, deixam o mesmo resto 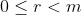 .
.
Se deixam o mesmo resto , então
, então 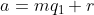 e
e 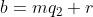 e a diferença
e a diferença 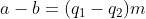 fornece uma nova interpretação:
fornece uma nova interpretação:
Exemplos: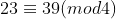 ,
,  e
e 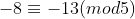
Quando não é congruente à
não é congruente à  , módulo
, módulo  , utilizamos
, utilizamos 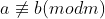 .
.
 Lema 1 : Se
Lema 1 : Se  é divisor de
é divisor de  , então podemos fazer
, então podemos fazer 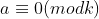 , porque
, porque  divide
divide 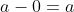 .
.
 Lema 2: Se
Lema 2: Se 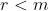 é o resto de
é o resto de 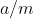 então
então 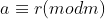 porque
porque 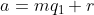 e
e  divide
divide 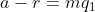 .
.
 Lema 3: Se
Lema 3: Se 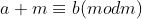 , então
, então 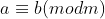 , porque
, porque  divide
divide 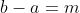 .
.
A relação de congruência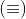 possui a maioria das propriedades ( ver art 048 ) da relação de igualdade
possui a maioria das propriedades ( ver art 048 ) da relação de igualdade 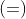 :
:
I)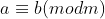
II) Se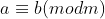 , então
, então 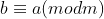
III) Se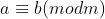 e
e 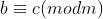 então
então 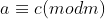
Dados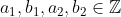 , nas operações de adição e multiplicação, temos:
, nas operações de adição e multiplicação, temos:
IV)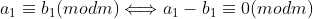
V) Se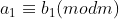 e
e 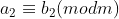 , então
, então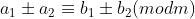
VI) Se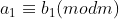 e
e 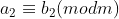 , então
, então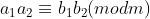
VII) Se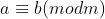 então
então 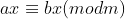 para todo
para todo 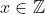 . No entanto, a recíproca não é de toda verdadeira: a propriedade do cancelamento vale apenas se
. No entanto, a recíproca não é de toda verdadeira: a propriedade do cancelamento vale apenas se 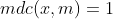 .
.
A Progressão Aritmética ( PA )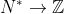 :
: 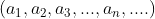 é um exemplo de congruência.
é um exemplo de congruência.
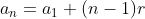 , sendo
, sendo 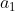 o primeiro termo e
o primeiro termo e  a razão.
a razão.
Como sabemos, a diferença de seus termos
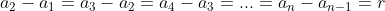
fornece sempre a razão e, portanto, todos os pares
e, portanto, todos os pares 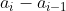 são divisíveis pela mesma. Assim,
são divisíveis pela mesma. Assim,
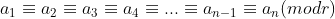
E pela propriedade III) conclui-se que, quaisquer que sejam  e
e 
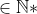 , teremos
, teremos 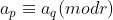 .
.
Se a PA tem o primeiro termo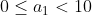 e razão
e razão 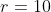 , então os últimos dígitos de todos os seus termos são iguais ao último dígito de
, então os últimos dígitos de todos os seus termos são iguais ao último dígito de 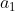 . Por exemplo, se
. Por exemplo, se 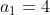 e
e 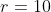 teremos a sucessão
teremos a sucessão 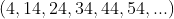 com os últimos dígitos de cada termo iguais ao último dígito do primeiro termo
com os últimos dígitos de cada termo iguais ao último dígito do primeiro termo 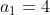 . Assim,
. Assim,
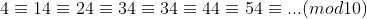
Isto ocorre devido a própria particularidade dos números escritos na base decimal que sempre tem o formato , com
, com 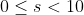 .
.
Ou seja, se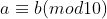 então
então  e
e  possuem os mesmos últimos dígitos.
possuem os mesmos últimos dígitos.
 Existe uma relação interessante entre a PA de razão
Existe uma relação interessante entre a PA de razão 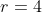 ( números congruentes módulo
( números congruentes módulo 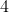 ), a PA de razão
), a PA de razão 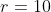 ( números congruentes módulo
( números congruentes módulo 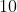 ) e as potências.
) e as potências.
Por exemplo, a sequência potencial definida por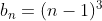 tem a particularidade que, a partir de
tem a particularidade que, a partir de 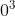 , os últimos dígitos dos seus termos se repetem periodicamente em
, os últimos dígitos dos seus termos se repetem periodicamente em 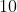 números, nesta ordem,
números, nesta ordem, 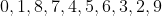 . O que, na linguagem de congruência:
. O que, na linguagem de congruência:
Na verdade, a sucessão 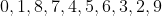 é válida para
é válida para 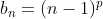 quando
quando 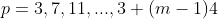 .
.
E, ao todo, temos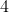 classes de sucessões de últimos dígitos para a sequência potencial
classes de sucessões de últimos dígitos para a sequência potencial 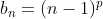 relativos à
relativos à 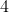 grupos de expoentes
grupos de expoentes  .:
.:
Classe 1: para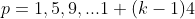
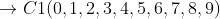
Classe 2: para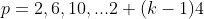
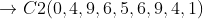
Classe 3: para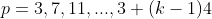
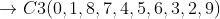
Classe 4: para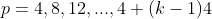
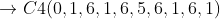
Para identificar a classe de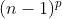 divide-se o expoente
divide-se o expoente  por
por 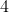 e se o resto for
e se o resto for 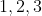 ou
ou  então a classe a qual pertence esta potência é classe
então a classe a qual pertence esta potência é classe  , classe
, classe  , classe
, classe 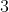 ou classe
ou classe 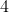 , respectivamente.
, respectivamente.
Dentro de uma mesma classe, todos os expoentes são congruentes módulo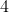 e podemos escrever o TEOREMA GERAL:
e podemos escrever o TEOREMA GERAL:
Se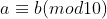 e
e  , então
, então 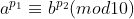
Justificativa: Em relação aos últimos dígitos de e
e 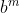
a sequência exponencial 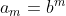 possui um padrão periódico horizontal conforme a seguir:
possui um padrão periódico horizontal conforme a seguir:
Passo1:
Passo2: Na coluna do B,
Passo3: O menor número do enquadramento (
Passo4: O último dígito de
Resposta
Porque este processo funciona? A resposta está nas RELAÇÕES DE CONGRUÊNCIA.
O conceito e a notação de congruência (
Dados
Diz-se que
Se deixam o mesmo resto
Exemplos:
Quando
A relação de congruência
I)
II) Se
III) Se
Dados
IV)
V) Se
VI) Se
VII) Se
A Progressão Aritmética ( PA )
fornece sempre a razão
Se a PA tem o primeiro termo
Isto ocorre devido a própria particularidade dos números escritos na base decimal que sempre tem o formato
Ou seja, se
Por exemplo, a sequência potencial definida por
Se 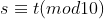 então
então 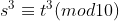 , para
, para  e
e 
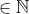 .
.
E, ao todo, temos
Classe 1: para
Classe 2: para
Classe 3: para
Classe 4: para
Para identificar a classe de
Dentro de uma mesma classe, todos os expoentes são congruentes módulo
Se
Justificativa: Em relação aos últimos dígitos de
De forma que, se na horizontal temos os padrões 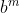 , na vertical são formadas as
, na vertical são formadas as 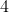 classes de
classes de 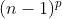 .
.
Problema: Qual o último dígito de 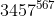 ? . Resolução: dividindo
? . Resolução: dividindo 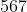 por
por 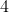 , encontramos o resto
, encontramos o resto 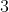 , logo, pelo lema 2,
, logo, pelo lema 2, 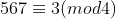 o que indica que esta potência pertence à classe
o que indica que esta potência pertence à classe 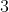 :
: 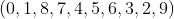 . Como
. Como 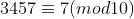 , então
, então 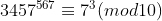 e, pelos elementos da classe
e, pelos elementos da classe 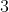 , vimos que
, vimos que 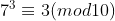 .
.
Resumo: De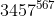 ,
, 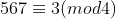 e
e 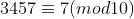

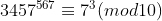
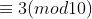 .
.
Resposta: o último dígito de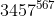 é
é 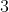 .
.
Resumo: De
Resposta: o último dígito de
Observação: Como podem ver pelos grupos de expoentes  e pelas classes C de sucessão dos últimos dígitos de
e pelas classes C de sucessão dos últimos dígitos de 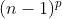 é também fácil calcular, de memória, as raízes quínticas de números
é também fácil calcular, de memória, as raízes quínticas de números 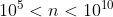 e raízes sétimas de números
e raízes sétimas de números 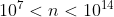 , com um método semelhante ao descrito no início desta postagem, bastando para isso, fazer um ajuste na tabela.
, com um método semelhante ao descrito no início desta postagem, bastando para isso, fazer um ajuste na tabela.
Fonte ( congruências ):
Teoria dos Números, de
Salahoddin Shokranian,
Marcus Soares,
Hemar Godinho;
Editora UNB, 1998.
Fonte ( congruências ):
Teoria dos Números, de
Salahoddin Shokranian,
Marcus Soares,
Hemar Godinho;
Editora UNB, 1998.



Excelente post! Ele pode ser uma das respostas a pergunta: Para que servem as congruências modulares? Parabéns por compartilhar este assunto conosco.
ResponderExcluirAlgum tempo atrás tive a ilusão de demonstrar o Último Teorema de Fermat com esta teoria ( rs ). Obrigado e seja sempre bem-vindo!
ResponderExcluirOu melhor, a ilusão de querer demonstrar....
ResponderExcluirGostei do post. Eu não conhecia muita coisa sobre congruências modulares. Aqui deu para entender bastante coisa de forma simples.
ResponderExcluirUm abraço.
Kleber, a congruência está bastante presente em nossas vidas e é um atalho para provar muitos teoremas ligados a Teoria dos Números. Este assunto que abordei fica interessante de mudarmos a base numérica. Surgirão outras classes e o TEOREMA GERAL se "deformará", mas na essência, permanecerá o mesmo. Valeu!
ResponderExcluirOlá Aloísio. As congruências são bem interessantes. Curiosamente eu estava preparando uma postagem sobre este tema. Mas eu ia mostrar como utilizá-las para demonstrar alguns critérios de divisibilidade.
ResponderExcluirAbraço.
Pedro R.
Pedro R., eu acho que os internautas estão precisando de uma matéria de qualidade sobre critérios de divisibilidade. Principalmente para os números primos. Obrigado pela visita!
ResponderExcluirOlá, Aloísio!!!!
ResponderExcluirAchei superinteressante o seu post e como é o primeiro da listagem desse carnaval, é o que me dedico a ler e comentar! Rapaz, que coisa boa isso aqui!!! Lembrei dos tempos da universidade quando estudava álgebra!!
Logo no início do post, pensei que aquilo era (e não deixa de ser) uma matemágica para se responder de cabeça o valor da raiz cúbica de um número de até cinco dígitos e que seja um cubo perfeito!!!
Relembrando essas clsses, me disparou um pensamento que a classe de módulo 4, poderá ser usada para se tentar prever a sua saída (probabilidade) por ocasião de um próximo sorteio, tipo... a mega sena!!! Mas, não vou tentar me debruçar sobre isso agora, o importante é que a matéria do seu artigo me indicou isso!!
Então, meus parabéns pelo artigo, pela presença no evento e pela continuação das postagens no blog Elementos de Teixeira!!!!
Um abraço!!!!!
Oi, Valdir!
ExcluirObrigado pelo incentivo!
Ainda não vizualizei este emprego das classes módulo 4 conforme mencionou. Mas fico contente quando um artigo meu fornece uma luz sobre um novo assunto.
Um grande abraço!