Neste artigo, veremos a justificativa do porque o número de divisores de 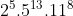 é
é 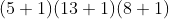 . Veremos também um atalho eficaz para calcular a soma dos divisores positivos de qualquer número primo ou composto, assim como o cálculo da soma das potências destes divisores.
. Veremos também um atalho eficaz para calcular a soma dos divisores positivos de qualquer número primo ou composto, assim como o cálculo da soma das potências destes divisores.
Para estas operações, apresento aos leitores a função aritmética multiplicativa.
Para estas operações, apresento aos leitores a função aritmética multiplicativa.
Função aritmética  é uma função
é uma função 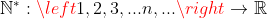 cuja lei de formação depende de
cuja lei de formação depende de  .
.
TEOREMA 1
Se  é multiplicativa e se
é multiplicativa e se 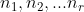 são inteiros positivos, onde cada um não tem fatores primos em comum com qualquer outro (
são inteiros positivos, onde cada um não tem fatores primos em comum com qualquer outro ( 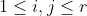 ,
, 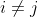 e
e 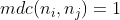 ) , então
) , então
O que este teorema diz é que se a propriedade da função aritmética multiplicativa é válida para  fatores ( por definição ), então ela é válida para qualquer quantidade
fatores ( por definição ), então ela é válida para qualquer quantidade  de fatores, desde que sejam cumpridas as condições de primalidade entre eles.
de fatores, desde que sejam cumpridas as condições de primalidade entre eles.
Demonstração: será por indução. Suponha que o teorema seja verdadeiro para algum 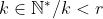 . Com esta hipótese, mostrarei que ele é válido para
. Com esta hipótese, mostrarei que ele é válido para 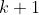 e, como consequência, a validade será estendida para
e, como consequência, a validade será estendida para  . Se não, vejamos. Seja
. Se não, vejamos. Seja
Pela condição 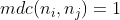 , o produto
, o produto 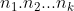 não tem fatores primos comuns com
não tem fatores primos comuns com 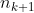 . Portanto,
. Portanto, 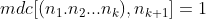 . Pela definição de função aritmética multiplicativa e junto com a hipótese de indução, temos
. Pela definição de função aritmética multiplicativa e junto com a hipótese de indução, temos
Observação:
esta técnica de demostração se chama PRINCÍPIO DE INDUÇÃO. É
talvez o mais importante método indireto de prova matemática. Serve para provar
proposições que dependem de 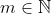 . Semelhante ao "efeito dominó": derrubando um dominó de uma fileira de dominós, todos os posteriores caem.
. Semelhante ao "efeito dominó": derrubando um dominó de uma fileira de dominós, todos os posteriores caem.
TEOREMA 2
A função aritmética 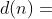 número de divisores positivos de
número de divisores positivos de  é multiplicativa.
é multiplicativa.
Demonstração: seja  e
e 
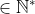 na condição
na condição 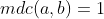 . Sendo
. Sendo 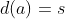 e
e 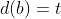 , os conjuntos dos divisores de
, os conjuntos dos divisores de  e
e  são:
são:
Como 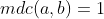 ,
,  e
e  não possuem fatores primos em comum. Assim, qualquer divisor do produto
não possuem fatores primos em comum. Assim, qualquer divisor do produto 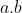 será um número da forma
será um número da forma 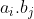 , com
, com 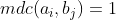 onde
onde 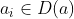 e
e 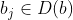 . Como temos
. Como temos  possiblidades para os divisores
possiblidades para os divisores 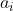 de
de  e
e  possibilidades para os divisores
possibilidades para os divisores 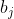 de
de  , temos então
, temos então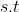 possibilidades para os divisores
possibilidades para os divisores 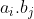 de
de 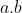 . Logo,
. Logo, 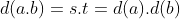 provando que
provando que 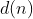 é uma função aritmética multiplicativa.
é uma função aritmética multiplicativa.
Observação: para  primo e
primo e 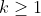 natural , temos
natural , temos 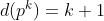 , porque os únicos divisores da potência de um número primo são
, porque os únicos divisores da potência de um número primo são 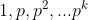 . Assim, sendo
. Assim, sendo 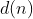 uma função aritmética multiplicativa, podemos calcular
uma função aritmética multiplicativa, podemos calcular 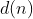 , para qualquer
, para qualquer  , conforme o exemplo a seguir.
, conforme o exemplo a seguir.
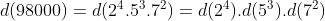
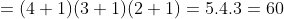
TEOREMA 3
A função aritmética 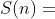 soma dos divisores positivos de
soma dos divisores positivos de  é multiplicativa.
é multiplicativa.
Demonstração: utilizando as definições da demostração do teorema anterior, vamos mostrar que 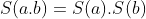 , com
, com 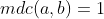 . Os divisores do produto
. Os divisores do produto 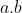 são da forma
são da forma 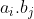 , onde
, onde 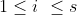 e
e 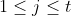 , onde
, onde  e
e  são os números de divisores de
são os números de divisores de  e
e  , respectivamente. Nestas condições, a soma
, respectivamente. Nestas condições, a soma 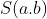 dos divisores de
dos divisores de 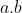 será:
será:
Colocando 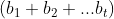 em evidência,
em evidência,
Exemplo: ( lembrem-se que, para  primo,
primo, 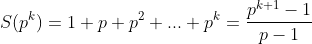 ).
).
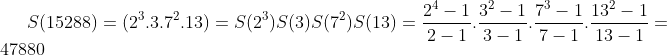 .
.
 O teorema a seguir será útil para a soma das potências dos divisores positivos de
O teorema a seguir será útil para a soma das potências dos divisores positivos de  .
.
TEOREMA 4
Se
a) 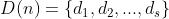 é o conjunto de divisores de
é o conjunto de divisores de  e
e
b) 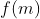 é uma função aritmética multiplicativa qualquer.
é uma função aritmética multiplicativa qualquer.
então a função aritmética definida por 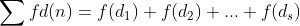 é também multiplicativa, ou seja, dados
é também multiplicativa, ou seja, dados  e
e  inteiros positivos tais que
inteiros positivos tais que 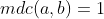 , temos
, temos
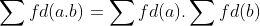
e o produto destes dois resultados,
..............................................................................
.........................................................................................
Como
..........................................................................
PROBLEMA 1
Com  primo,
primo,  natural
natural 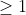 e
e 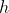 natural
natural 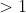 , calcular a soma das
, calcular a soma das 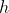 -ésimas potências dos divisores de
-ésimas potências dos divisores de 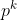 .
.
Resolução: os divisores de 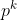 são
são 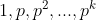 e suas
e suas 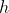 -ésimas potências
-ésimas potências 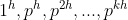 formam uma
formam uma 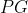 com primeiro termo
com primeiro termo 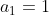 e razão
e razão 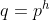 . Portanto,
. Portanto,
para 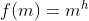 , temos
, temos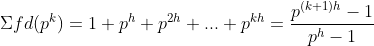
PROBLEMA 2
Calcular a soma dos cubos dos divisores de 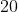 .
.
Resolução: o que queremos é 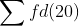 com
com 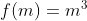 . Ora,
. Ora, 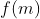 é uma função aritmética (totalmente) multiplicativa porque para
é uma função aritmética (totalmente) multiplicativa porque para 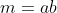 ,
, 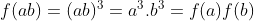 . E se ainda
. E se ainda 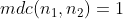 pelo teorema 4, temos,
pelo teorema 4, temos, 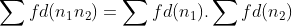 caracterizando a multiplicabilidade (restrita) de
caracterizando a multiplicabilidade (restrita) de 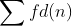 para
para 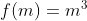 . Logo,
. Logo,
REFERÊNCIA BIBLIOGRÁFICA
- Funções Aritméticas - Números Notáveis, de Edgard de Alencar Filho, Editora Nobel,1988
- Teoria dos Números, de Salahoddin Shokranian, Marcus Soares, Hemar Godinho; Editora UNB, 1998.


Cada dia que passa Elementos de Teixeira fica mais iteressante!
ResponderExcluirContinue assim!
ResponderExcluirObrigado, matemático Hunasses! Em breve verei uma teoria sua aqui publicada!
ResponderExcluir