A derivada geométrica aplicada em uma progressão geométrica ordinária ( ) definida por
) definida por 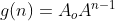 é
é
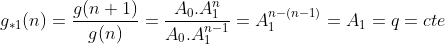
Assim a derivada  de uma
de uma 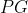 ordinária é uma função aritmética constante
ordinária é uma função aritmética constante 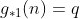 cujo valor é a própria razão da mesma.
cujo valor é a própria razão da mesma.
INTEGRAL GEOMÉTRICA ou integral é a operação inversa da derivada
é a operação inversa da derivada  de forma que se existir uma função aritmética definida por
de forma que se existir uma função aritmética definida por 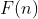 , onde
, onde 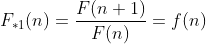 , então
, então 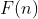 é a integral
é a integral  de
de 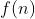 . Simboliza-se
. Simboliza-se 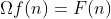 e
e 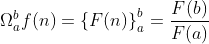 , onde
, onde 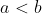 são considerados limites racionais.
são considerados limites racionais.
INTEGRAL GEOMÉTRICA ou integral
PROGRESSÃO GEOMÉTRICA DE ORDEM 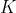 ou
ou 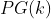 é uma função aritmética definida por
é uma função aritmética definida por
com 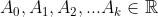 e
e 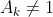 .
.
TEOREMA
Se 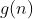 é uma
é uma 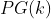 conforme ( 1 ), então sua derivada
conforme ( 1 ), então sua derivada  é
é
Comparando ( 1 ) e ( 2 ), vemos que:
1) Se 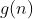 tem ordem
tem ordem  , então
, então 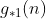 tem ordem
tem ordem 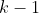 .
.
2) Os coeficientes de 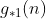 são os mesmos de
são os mesmos de 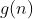 , com exceção de
, com exceção de 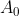 , mas transladados de um fator para a esquerda.
, mas transladados de um fator para a esquerda.
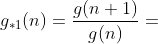
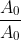
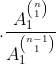
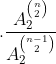
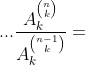
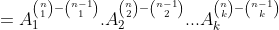
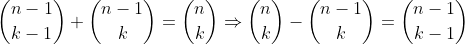
DEMONSTRAÇÃO
Agora, lembrem-se que a soma de duas células consecutivas 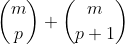 do triângulo de Pascal resulta numa célula da linha seguinte
do triângulo de Pascal resulta numa célula da linha seguinte 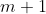 e da mesma coluna
e da mesma coluna 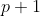 , ou seja,
, ou seja, 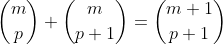 ( RELAÇÃO DE STIFFEL ). Fazendo
( RELAÇÃO DE STIFFEL ). Fazendo 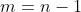 e
e 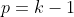 a relação fica
a relação fica
Logo, temos ( 2 ): 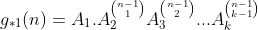
NOTAÇÃO DAS DERIVADAS  SUCESSIVAS DE
SUCESSIVAS DE 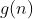
.........................................................................................................................
.........................................................................................................................
Neste caso, 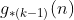
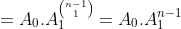
Assim,  , é uma
, é uma  de ordem
de ordem  , o resultado da aplicação da derivada
, o resultado da aplicação da derivada  em
em  ,
, 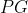 de ordem
de ordem  .
.
Portanto,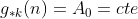 . E para todo
. E para todo 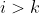 temos
temos 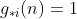 .
.
INVESTIGAÇÃO DAS BASES 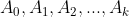
Para 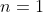 , temos
, temos 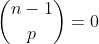 , visto que
, visto que 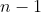 é fator de
é fator de 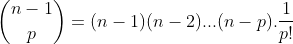 . Em consequência, os valores das bases
. Em consequência, os valores das bases 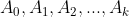 são calculados conforme a seguir.
são calculados conforme a seguir.
...............................................................................................................
...............................................................................................................
Logo, 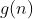 pode ser reescrita como
pode ser reescrita como
Exemplo de obtenção das bases. Seja a 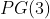 definido por
definido por 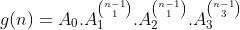 . Se seus
. Se seus 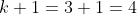 valores iniciais são
valores iniciais são 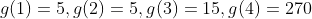 , podemos fazer um triângulo numérico onde a razão entre duas células consecutivas ( direita pela esquerda ) de uma mesma linha resulta na célula do meio da linha inferior. Veja:
, podemos fazer um triângulo numérico onde a razão entre duas células consecutivas ( direita pela esquerda ) de uma mesma linha resulta na célula do meio da linha inferior. Veja:
Pegamos, então, as bases 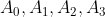 na diagonal esquerda deste triângulo numérico:
na diagonal esquerda deste triângulo numérico:
Logo,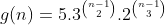 , já que
, já que 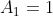
Observação: a função aritmética finita cujos valores são
PRODUTO 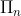 DOS
DOS  PRIMEIROS TERMOS DE UMA FUNÇÃO ARITMÉTICA QUALQUER
PRIMEIROS TERMOS DE UMA FUNÇÃO ARITMÉTICA QUALQUER
Seja 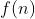 uma função aritmética qualquer. Se existir
uma função aritmética qualquer. Se existir 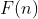 (
( 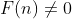 ) tal que
) tal que 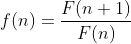 então
então
E, após o cancelamento de numeradores com denominadores iguais,concluímos que
ou seja, o produto 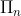 dos
dos  primeiros termos de uma função aritmética qualquer
primeiros termos de uma função aritmética qualquer 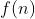 é a integral
é a integral 
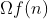 desta sequência nos limites racionais
desta sequência nos limites racionais 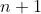 e
e  .
.
PRODUTO 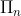 DOS
DOS  PRIMEIROS TERMOS DE UMA
PRIMEIROS TERMOS DE UMA 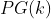
Se a derivada  de
de 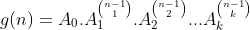 é
é
então, por indução inversa, podemos dizer que a integral  de
de 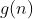 é
é
onde  é uma constante real arbitrária chamada de constante de integração geométrica. Logo, como
é uma constante real arbitrária chamada de constante de integração geométrica. Logo, como 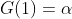 , temos
, temos


kade a soma dos n primeiros termos?
ResponderExcluir