A menor velocidade para que um corpo, impulsionado de baixo para cima na superfície terrestre, escape teoricamente da gravidade de nosso planeta é
Em um lançamento na vertical com uma velocidade inicial 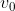 , a expressão que relaciona a velocidade
, a expressão que relaciona a velocidade  final do corpo com a distância
final do corpo com a distância  do mesmo ao centro do globo é
do mesmo ao centro do globo é
demonstrada no blog parceiro FATOS MATEMÁTICOS .
Na fórmula, percebe-se que, quando  é muito grande, o resultado de
é muito grande, o resultado de 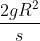 se torna desprezível. Matematicamente , temos que, quando
se torna desprezível. Matematicamente , temos que, quando 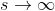 , então
, então 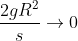 .
.
Decorre que, com 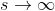 , surge uma expressão limite de
, surge uma expressão limite de  , que é
, que é
Como podemos interpretar este modelo matemático, ou seja, a expressão limite  , à luz da mecânica clássica? Quer dizer que, hipoteticamente no infinito ( distância
, à luz da mecânica clássica? Quer dizer que, hipoteticamente no infinito ( distância  infinita ), se um corpo está teoricamente livre do campo gravitacional terrestre e de outros campos gravitacionais, então, conforme a primeira lei de Newton, ou o corpo está em repouso ou em movimento retilíneo uniforme (
infinita ), se um corpo está teoricamente livre do campo gravitacional terrestre e de outros campos gravitacionais, então, conforme a primeira lei de Newton, ou o corpo está em repouso ou em movimento retilíneo uniforme (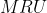 ) com velocidade escalar final de
) com velocidade escalar final de 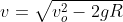 . Na situação de repouso, temos
. Na situação de repouso, temos  , que é a nossa velocidade de escape, definida no início do post.
, que é a nossa velocidade de escape, definida no início do post.
 Agora, vamos obter as expressões horárias de
Agora, vamos obter as expressões horárias de  e
e  , durante a viagem de escape ( com a velocidade inicial mínima para a mesma ).
, durante a viagem de escape ( com a velocidade inicial mínima para a mesma ).
No processo de lançamento, na superfície terrestre, temos
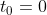 ,
, 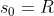 e
e 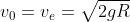
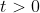 ,
, 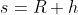 e
e 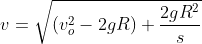
No processo de lançamento, na superfície terrestre, temos
E, em algum ponto da subida, temos
Mas, como adotamos 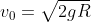 , temos
, temos 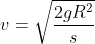 e, portanto,
e, portanto,
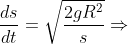
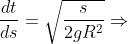
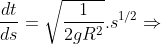
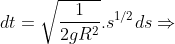
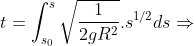
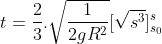
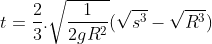 (1)
(1)
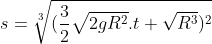 (2)
(2)
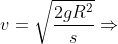
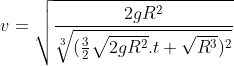 (3)
(3)
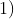 Com a expressão (1) do tempo
Com a expressão (1) do tempo  em função de
em função de  , pode-se calcular, por exemplo, a duração da viagem Terra-Lua (centro a centro ) que levaria um corpo partindo da Terra com a velocidade inicial de escape
, pode-se calcular, por exemplo, a duração da viagem Terra-Lua (centro a centro ) que levaria um corpo partindo da Terra com a velocidade inicial de escape 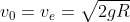 . Basta fazer
. Basta fazer  sendo a distância Terra-Lua. Fica como um interessante exercício proposto aos leitores.
sendo a distância Terra-Lua. Fica como um interessante exercício proposto aos leitores.
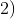 As expressões (2) e (3) são as funções horárias durante a viagem de escape. Observem que, nelas, quando
As expressões (2) e (3) são as funções horárias durante a viagem de escape. Observem que, nelas, quando 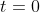 , temos
, temos 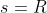 e
e 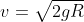 ( situação na posição inicial );
( situação na posição inicial );
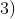 Todos os cálculos foram feitos considerando que a única força atuante no corpo em estudo é a da gravidade e que o planeta Terra é uma esfera perfeita.
Todos os cálculos foram feitos considerando que a única força atuante no corpo em estudo é a da gravidade e que o planeta Terra é uma esfera perfeita.
Referência bibliográfica
Cálculo com Geometria Analítica, Volume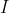 , Simmons, Editora McGraw-Hill, 1987.
, Simmons, Editora McGraw-Hill, 1987.
Referência na net.
http://fatosmatematicos.blogspot.com.br/2009/07/velocidade-de-escape.html
http://fatosmatematicos.blogspot.com.br/2010/08/o-tempo-de-impacto-de-um-meteoro.html
Gostará de ler também:
036-Densidade e Gravidade
035-O Planeta de Diamante
038-Geometria e Gravidade
032-Gravidade Zero?
058-O Problema dos Aviões e Outros Problemas/Questões
Imagem: http://ooleoondeesta.blogspot.com.br/2010/05/foguete-e-um-incansavel-pra-la-de.htm
Substituindo 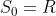 e desenvolvendo a integral definida, temos
e desenvolvendo a integral definida, temos
Agora, colocando  em função de
em função de  :
:
E  em função de
em função de  :
:
Observações
Referência bibliográfica
Cálculo com Geometria Analítica, Volume
Referência na net.
http://fatosmatematicos.blogspot.com.br/2009/07/velocidade-de-escape.html
http://fatosmatematicos.blogspot.com.br/2010/08/o-tempo-de-impacto-de-um-meteoro.html
Gostará de ler também:
036-Densidade e Gravidade
035-O Planeta de Diamante
038-Geometria e Gravidade
032-Gravidade Zero?
058-O Problema dos Aviões e Outros Problemas/Questões
Imagem: http://ooleoondeesta.blogspot.com.br/2010/05/foguete-e-um-incansavel-pra-la-de.htm


Olá Aloisio, vejo que suas ideias foram muito bem colocadas neste post. Percebo também, que você, assim como eu é um grande entusiasta da "Astronomia Matemática" em que inferimos sobre alguns acontecimentos astronômicos via as ferramentas da Matemática. Quanto ao e-mail com a fórmula, acho que não será necessário, pois elas já foram expostas acima. Buscarei publicar mais sobre o assunto. Além disso, agradeço pelos links e pela citação do blog acima. Um grande abraço.
ResponderExcluirObrigado, Paulo.
ResponderExcluirDe fato, um dos assuntos mais interessante para mim em Física Clássica é Gravitação Universal e os modelos matemáticos que dão forma às fórmulas envolvidas. Além do mais, sempre é gratificante a memória das obras do gigante Isaac Newton, consolidador das idéias de Copérnico, Kleper e Galileu em uma teoria colossal, válida até hoje para nosso cotidiano e fins práticos de engenharia, astronomia, automobilistica, etc.
Outro abraço!
Olá Aloísio, interessante este problema. Eu tentei fazer algumas contas para saber o tempo da Terra à Lua, como propôs em 1). Mas encontrei valores muito altos e creio que fiz alguma coisa errada.
ResponderExcluirConsiderei:
[;g=9,8m/s^2;]
[;R=6378000m;]
[;s=d_{TL}=380000000m;]
quando apliquei na fórmula
[;t= \frac{2}{3}.\sqrt{\frac{1}{2gR^2}} (\sqrt{s^3}-\sqrt{R^3} );]
[;t= \frac{2}{3}.\sqrt{\frac{1}{2\cdot 9,8 \cdot 6378000^2}} (\sqrt{380000000^3}-\sqrt{6378000^3} );]
encontrei um valor muito alto para o tempo: 440722970s, sugerindo que estou comendo bola em algum lugar. Tem alguma ideia?
Kleber: Posso estar enganado,mas acho que a partir de um certo ponto da trajetória bem longe da Terra, a gravidade da Lua passa a atuar, e aí deve dar uma diferencinha nos valores reais. Também estou achando estranho o valor do tempo encontrado nos seus cálculos. Acho que a partir de uma certa distância muito grande em relação à Terra, não sei se esta função do tempo se aplicaria sem que se cometesse um erro considerável. Será que não chega um instante em que os efeitos da gravidade da Terra são tão pequenos que, a partir deste ponto, a função do tempo,representada no post do Aloisio pela expressão (1) talvez começasse a apresentar distorções em relação aos valores reais?
ExcluirOi, Kleber,
ExcluirEu fiz assim,
[;t= \frac{2}{3}.\sqrt{\frac{1}{2\cdot 9,8 \cdot 6378000^2}} (\sqrt{380000000^3}-\sqrt{6378000^3} ) \Rightarrow;]
[;t=\frac{2}{3} sqrt{\frac{1}{797306126400000}}.(7407563702054,8125-16107449275,1645) \Rightarrow;]
[;t=\frac{2}{3} sqrt{\frac{1}{797306126400000}}.7391456252779,648 \Rightarrow;]
Mas como [;(7391456252779,648)^2=54633625536755355672526443,003904;] e passando para dentro do sinal de raíz, temos
[;t=\frac{2}{3}sqrt{\frac{54633625536755355672526443,003904}{797306126400000}}\Rightarrow;]
[;t=\frac{2}{3}.\sqrt{68522771527,465} \Rightarrow;]
[;t=\frac{2}{3}.261768,545=174512,363s=\frac{174512,363\ s}{86400\ s}\ dias \approx 2,019 \ dias;]
veja se não tropecei em alguma coisa.
Obrigado por tentar responder a questão.
Oi, Jairo,
Excluirno modelo que adotei, considerei, por exemplo apenas a distância Terra-Lua, sem considerar a Lua. Se eu levar en conta a Lua, o corpo chega em pouco menos de [;2;] dias com a velocidade de escape saindo da Terra, porque a atração da Lua ajuda no percurso.
Uma vez li que o homem chegou na Lua em torno de [;4;] dias. Acredito eu que esta demora se deu por causa de fatores técnicos e humanos.
Poxa Aloísio. Você foi longe nestas deduções! Eu fui até o post sobre velocidade de escape do blog do Prof.Paulo, que você linkou aí, e notei os primeiros comentários de lá, feitos antes dos seus, pelo Gustavo.O, que assim como eu, deve ser um professor de física do ensino médio. Ele mostra no comentário dele como chegar à fórmula da velocidade de escape, considerando energias. Tanto na dedução usando energias, que usamos para ensinar os alunos que ainda não conhecem o cálculo diferencial e integral, como na dedução usando integrais, tirada do livro de Simmons, considera-se a velocidade final nula, quando a variável (s) tende ao infinto. É interessante esta consideração, a partir do fato de que no infinito, estamos tão longe do referencial adotado (Terra) que parece não mais fazer sentido falarmos em uma diferença entre um objeto estar em repouso ou em MRU, pois sem um refencial, estes conceitos se equivalem. Posso estar viajando, mas me parece que aí possa estar a causa de nossas dúvidas, e provavelmente também, das interpretações do que seria movimento e repouso, sem um referencial proximo e claro. É que eu observei seus comentários no post do Prof.Paulo, e fiquei imaginando: Qual seria a causa do "erro" sobre considerar a velocidade final igual a zero. Sei lá, talvez pensando assim eu já esteja fugindo da física Newtoniana (clássica), que exige a adoção de um referencial claro para que se possa falar em movimento ou repouso.
ResponderExcluirNa verdade, esta situação de se lançar uma objeto verticamente para cima até que ele "saia" do campo gravitacional da Terra é bem diferente do que se faz na prática, quando um foguete é lançado para o espaço. O foguete é lançado na vertical, mas logo em seguida "deita-se", e a velocidade passa a ser tangencial, pois ele entra em órbita para que ele possa, aí sim, ir aumentando a velocidade até ser impulsionado para o espaço. Esta velocidade tangencial seria então, na prática, a velocidade tangencial limite de escape.
Bom. Acho que também acabei indo longe.
Abraço
Oi, Grossi,
ResponderExcluirAdmiro muito o seu espírito prático e questionador.
Nas minhas considerações, não tomei a Terra como referencial, mesmo porque ela é não-inércial ( não está em [;MRU;]).
As leis de Newton são válidas em um referencial inercial, mas é interessante notar que nas hipóteses da primeira lei não se cita nenhum referencial:
"Se um corpo está em um sistema isolado de forças externas, então o mesmo mestá em [;MRU;]."
Acredito, então, que o próprio sistema isolado citado na hipótese funcione com sistema inercial de referência, seja próximo a Terra ou muito distante dela. Acho que é isso.
Fez bem vc dar o exemplo do foguete. A imagem que coloque foi apenas ilustrativa. Valeu por esclarecer sobre a velocidade tangencial. Antes eu pensava que o foguete subia, a certa altura, com velocidade constante ( devido a força resultante ser nula da combinação da força de escape dos gazes, atrito do ar, peso do foguete, etc ) até sair da tmosfera terrestre.
Valeu!
Aloísio,
ResponderExcluirRefiz os cálculos usando o seu método de elevar ao quadrado e inserir na raiz para facilitar as contas. Encontrei um valor de 48h, equivalente ao seu.
No entanto, veja meu pensamento: Considerando a velocidade de escape igual a 11.300m/s, e que ela se mantém constante até a chegada de um foguete à Lua, e considerando a distância Terra-Lua igual a 380.000.000m, com uma regra de três simples chega-se ao valor de 33.628 segundos, que é cerca de 9,3 horas, que é um valor muito diferente do encontrado inicialmente, que é de cerca de 2 dias. No entanto, quando chega no espaço e fica livre da ação gravitacional da Terra, acredito que essa velocidade aumente ainda mais e assim diminuiria ainda mais o tempo gasto até a Lua.
Levei em consideração o fato de não haver gravidade e atrito
Entendi o que quis dizer Kleber,mas a velocidade de escape é apenas o impulso inicial e, a partir daí, a gravidade começa a atuar e diminuir a velocidade até a chegada ao ponto que coincide com a distância Terra-Lua. De acordo com o segundo link do Paulo, só para ter uma idéia, um corpo caindo da Lua leva uns 6 dias para chegar à Terra...
ResponderExcluir