progressão mista é a sequência numérica 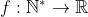 , onde
, onde
Cada termo, a partir do segundo, é igual ao anterior vezes uma constante  e mais uma constante
e mais uma constante  , ou seja
, ou seja
Ou então, cada termo, a partir do segundo, é igual ao anterior mais uma constante  e vezes uma constante
e vezes uma constante  , ou seja,
, ou seja,
As constantes  e
e  ( ou
( ou  ) são denominadas razão multiplicativa e aditiva da progressão mista, respectivamente.
) são denominadas razão multiplicativa e aditiva da progressão mista, respectivamente.
O segundo conceito é equivalente ao primeiro, pois temos
Logo, para cada  onde
onde 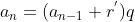 , existirá um
, existirá um  tal que
tal que 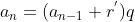 . De fato, pois
. De fato, pois 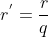 .
.
Adotaremos a primeira definição com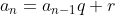 .
.
Adotaremos a primeira definição com
Exemplo
Sejam 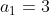 ,
, 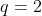 e
e 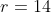 .
.
Formaremos os quatro primeiros termos da progressão mista de duas formas: com
Cálculo das razões  e
e 
Do sistema
tiramos
com
( fornecida pela primeira equação do sistema )
Assim, precisamos de três termos consecutivos 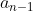 ,
, 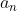 e
e 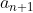 para acharmos as razões
para acharmos as razões  e
e  da progressão mista.
da progressão mista.
Calcular as razões da progressão mista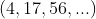 . Temos, então,
. Temos, então, 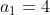 ,
, 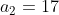 e
e 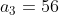 . Logo,
. Logo,
Exemplo
Calcular as razões da progressão mista
Sendo possível estes cálculos, concluímos que, dados três números quaisquer que não estejam em 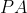 ou
ou 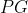 , então estes números sempre farão parte de uma progressão mista.
, então estes números sempre farão parte de uma progressão mista.
Pela relação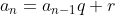 , temos
, temos
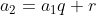
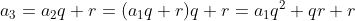
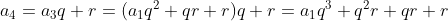
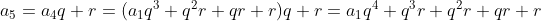
![.................................................................................................................. [;..................................................................................................................;]](https://thewe.net/tex/..................................................................................................................)
![.............................. [;..............................;]](https://thewe.net/tex/..............................)
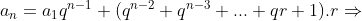
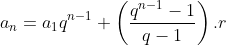
Fórmula do termo geral
Pela relação
Exemplos
Assim, a sequência do primeiro exemplo 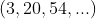 , com
, com 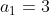 ,
,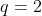 e
e 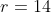 fica
fica
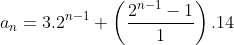
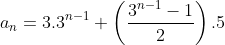
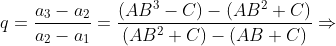
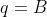
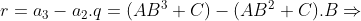

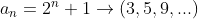 , com
, com  ,
,  e
e 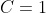
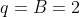
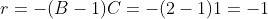
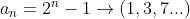 , com
, com 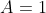 ,
, 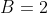 e
e 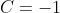
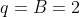
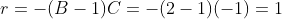
Enquanto que a sequência do segundo exemplo 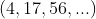 , com
, com 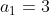 ,
, 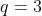 e
e 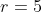 tem a forma
tem a forma
Considerações sobre o termo geral - forma sintética
Com um pequeno rearranjo, a fórmula 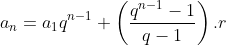 se transforma em
se transforma em
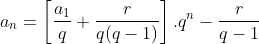
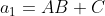 ,
, 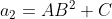 e
e 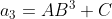
e chegamos a forma sintética 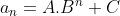 , com
, com
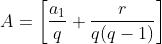 ,
, 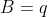 e
e 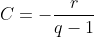
Na forma sintética, temos
Assim,
Exemplos 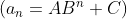
Curiosidades
A fórmula que fornece a soma dos  primeiros termos de uma progressão geométrica (
primeiros termos de uma progressão geométrica (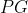 ), de primeiro termo
), de primeiro termo 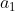 e razão
e razão 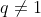 , ou seja,
, ou seja, 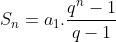 , é o enésimo termo de uma progressão mista. De fato,
, é o enésimo termo de uma progressão mista. De fato,
com 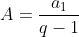 ,
, 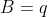 e
e 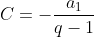 , sendo
, sendo
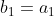
A sequência constante
Sugestão de pesquisa
Gostará de ler também:
Referência bibliográfica: Coleção Fundamentos de Matemática Elementar-V4.
Imagem: http://www.fractal.org/Fractal-tree-scaffold.htm


Oi Teixeira!Suponhamos que eu tome um empréstimo de a0 reais em n prestações mensais a uma taxa de i% ao mês e os juros correm todo mês. Eu pago todo mês uma prestação de r reais. Qual a dívida que eu tenho em cada mês? Seja q=1+i/100, a dívida do primeiro mês é a1=a0q - r, a dívida do segundo mês é a2=a1q - r. Se não soubermos o valor da prestação para calcularmos basta igualar a dívida a zero no termo geral. abçs
ResponderExcluirOi, Tavano!
ResponderExcluirMuita boa esta aplicação de progressão mista. Seu comentário foi um complemento essencial ao post.
Desconfio que, se existisse fórmula fechada para a soma dos n primeiros termos de uma progressão geométrica de segunda ordem, então ela seria parecida com a equação da sugestão para pesquisa que dei ao final do artigo.
Sobre soma de dois quadrados da forma a^2+b^2=4k+1, me enganei a respeito do livro que tenho, pois eram apenas teoremas de existência. Mas no blog FATOS MATEMATICOS, temos uma matéria interessante sobre isto.
Veja em http://fatosmatematicos.blogspot.com.br/2011/02/representacao-dos-naturais-como-soma-de.html.
O artigo também foi publicado no Carnaval UBM 14.
Valeu, um abraço.
Caro Teixeira! Embora o blog indicado não tenha a resposta, como sempre no "FATOS MATEMÁTICOS" aprendi muito sobre o assunto (a^2+b^2=P). O motivo da pergunta é que eu tinha desenvolvido um método para achar "a" e "b" e embora não tivesse conseguido demonstrá-lo estava convencido de que funcionava, ontem percebi o porquê, achei um contraexemplo para p=89. O método era interessante: Dado p=4k+1 (por exemplo 41) eu devia encontrar j tal que j^2+1==0(mód p)(para p=41, j=9)encontrado j (um pouco difícil e trabalhoso) eu dividia p por j e o quociente e o resto dessa divisão eram o "a" e o "b" (no caso para 41=9.4 + 5=>4^2 + 5^2=41) Talvez ainda dê para consertar. Obs há dois "jotas" toma-se o menor. Obrigado pelo espaço. Abçs.
ExcluirO latex não tá funcionando! :O
ResponderExcluir