Publicado no ano de
Cardano não foi solucionador de nenhuma destas equações. No entanto, a solução da cúbica é hoje em dia comumente chamada de fórmula de Cardano. As vezes, também é chamada de fórmula de Cardano-Tartaglia, homenageando o publicador e o descobridor. Já a solução da quártica é chamado acertadamente de método de Ferrari.
Tartaglia Ferrari
O italiano Nicoló Fontana) ou Tartaglia (gago) foi um desafortunado na infância, um gênio competidor e azarado na vida adulta. Envolvido em disputas matemáticas com apostas, Tartaglia descobriu a solução da cúbica e isto o levou a ter grande vantagem sobre seus adversários. Teve o desprazer de conhecer Cardano que levava uma vida financeiramente melhor e, portanto, sua única preocupação era com a fama. Através de palavras de convencimento e juras de segredo, Cardano conseguiu a fórmula da cúbica de Tartaglia e esquecendo todas as promessas, a publicou em Ars Magna. No entanto, com créditos a Tartaglia. Mesmo assim, os dois se tornaram inimigos.
ou Tartaglia (gago) foi um desafortunado na infância, um gênio competidor e azarado na vida adulta. Envolvido em disputas matemáticas com apostas, Tartaglia descobriu a solução da cúbica e isto o levou a ter grande vantagem sobre seus adversários. Teve o desprazer de conhecer Cardano que levava uma vida financeiramente melhor e, portanto, sua única preocupação era com a fama. Através de palavras de convencimento e juras de segredo, Cardano conseguiu a fórmula da cúbica de Tartaglia e esquecendo todas as promessas, a publicou em Ars Magna. No entanto, com créditos a Tartaglia. Mesmo assim, os dois se tornaram inimigos.
Cardano
Tartaglia Ferrari
O italiano Nicoló Fontana
O também italiano Ludovico Ferrari ) , com condições extremamentes precárias na infância e juventude, este sim teve sorte de conhecer Cardano. O mesmo chamou Ferrari, então com
, com condições extremamentes precárias na infância e juventude, este sim teve sorte de conhecer Cardano. O mesmo chamou Ferrari, então com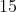 anos, para trabalhar como servo e logo depois como secretário. O motivo disso é que Cardano tinha notado qualidades naquele jovem, particularmente na matemática. Quando publicou a solução da quártica na Ars Magna, Cardano fez a seguinte referência: " foi inventado por Ludovico Ferrari, ao meu pedido".
anos, para trabalhar como servo e logo depois como secretário. O motivo disso é que Cardano tinha notado qualidades naquele jovem, particularmente na matemática. Quando publicou a solução da quártica na Ars Magna, Cardano fez a seguinte referência: " foi inventado por Ludovico Ferrari, ao meu pedido".
Tanto a solução da cúbica quanto da quártica possuem apenas valor histórico porque levam à formatos numéricos desajeitados para o homem prático moderno que dispõe de calculadoras e computadores, onde o método de Newton é de mais agradável utilização, por exemplo. Sendo assim, postarei aqui apenas a estratégia de resolução ( o caminho ) destas equações. Estes são casos interessantes onde o processo tem mais valor que o produto final.
SOLUÇÃO DA EQUAÇÃO CÚBICA COMPLETA
Seja a equação cúbica
Fazendo 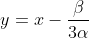 e dividindo ambos os membros da transformada pelo coeficiente de
e dividindo ambos os membros da transformada pelo coeficiente de 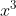 , obtemos
, obtemos
Seja agora
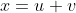 , logo
, logo
^3%20\Rightarrow)
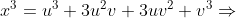
+v^3%20\Rightarrow)
+v^3%20\Rightarrow)
-(u^3+v^3)=0)
Comparando com
Comparando com
temos a seguinte equivalência dos coeficientes: 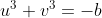 e
e 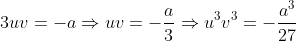 , de forma que o sistema
, de forma que o sistema
é do 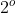 em
em 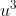 e
e 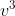 de fácil resolução.
de fácil resolução.
Acha-se 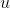 e
e  , segue que
, segue que 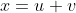 e finalmente
e finalmente 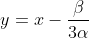 .
.
SOLUÇÃO DA EQUAÇÃO QUÁRTICA COMPLETA
Seja a equação quártica
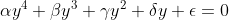
Fazendo 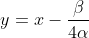 e dividindo ambos os membros da transformada pelo coeficiente de
e dividindo ambos os membros da transformada pelo coeficiente de 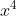 , obtemos
, obtemos
Completando o quadrado no primeiro membro,
A técnica do complemento do quadrado é conhecida desde o Antigo Egito. Porém, mesmo sendo necessária, é insuficiente para resolver a quártica. O grande deslumbre de Ferrari foi introduzir uma constante  inicialmente desconhecida da seguinte forma:
inicialmente desconhecida da seguinte forma:
O próximo passo é escolher  de forma que o segundo membro também seja um trinômio quadrado perfeito. Isto acontecerá quando o discriminante delta relativo à expressão quadrática em
de forma que o segundo membro também seja um trinômio quadrado perfeito. Isto acontecerá quando o discriminante delta relativo à expressão quadrática em  do segundo membro for
do segundo membro for 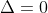 . Observem os leitores que este estratagema não é um complemento de quadrado mas sim um ajustamento de coeficientes. Portanto, é necessário que
. Observem os leitores que este estratagema não é um complemento de quadrado mas sim um ajustamento de coeficientes. Portanto, é necessário que
(k^2+ak+e)=0)
+k\right]^2=(fx+g)^2%20\Rightarrow)
+k=fx+g)
e temos uma equação em  , chamada de cúbica resolvente, cuja solução se consegue pela fórmula de Cardano-Tartaglia.
, chamada de cúbica resolvente, cuja solução se consegue pela fórmula de Cardano-Tartaglia.
Acha-se  , o segundo membro torna-se um quadrado perfeito,
, o segundo membro torna-se um quadrado perfeito,
e chegamos à uma equação quadrática em  .
.
Calcula-se  e finalmente
e finalmente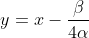 .
.
_*_
Em simbologia moderna, podemos perceber com facilidade as belas estratégicas usadas na cúbica e na quártica. Mas Cardano expôs estas soluções na Ars Magna verbalmente, como se fosse uma "receita" ( faça isso, tire aquilo, etc ). Quem quiser conhecer esta obra na íntegra, segue o link: http://www.e-rara.ch/zut/content/pageview/2690143
Gostará de ler também:
078-Fórmulas de Bhaskara e Cardano pelas Relações de Girard-Método de Tavano
090-Equações Recíprocas ( Parte 3/3 )
092-Disquisitiones Arithmeticae de Gauss
Referência Bibliográfica:
Imagens:
-O Romance das Equações Algébricas, de Gilberto G.Garbi, Editora Makron Books, 1997;
-História da Matemática de Carl.B.Boyer, Editora Edigard Blücher LTDA, 1974. Imagens:
http://www.e-rara.ch/
http://www.nndb.com/people/440/000098146/
http://www.profcardy.com/matematicos/individuos.php?pid=198
http://gaussianos.com/la-semana-de-la-cubica-la-historia-de-su-resolucion/





Acho que eu e muitos outros que estão na Matemática hoje foram atraídos com um método de resolução da equação do terceiro grau. Li a história no excelente livro O Romance das Equações Algébricas e vi que no mundo da Matemática existe muita inveja, injustiça e roubo de fórmulas. Parabéns pela postagem esclarecedora o qual garanto que irá atrair muitas outras pessoas para a Matemática.
ResponderExcluirOi, Paulo!
ExcluirAs quínticas foram examinadadas com mais ênfase logo após o surgimento de Ars Magna. Acredito que, no percurso até Abel e Galois, muito matemática boa foi produzida.
Um abraço!