Fiz este estudo em  sobre uma questão que me foi proposta por meu sobrinho Hunasses Souza, de Fortaleza / CE.
sobre uma questão que me foi proposta por meu sobrinho Hunasses Souza, de Fortaleza / CE.
Considere a seguinte sequência numérica:
Observem que nela existem subsequências do tipo ) , onde
, onde 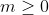 , de forma que a cada recontagem de
, de forma que a cada recontagem de  em
em  , o número de termos
, o número de termos  de
de  fica acrescido de uma unidade.
fica acrescido de uma unidade.
Como calcular o enésimo termo de  ? Ou melhor, qual a fórmula do termo geral
? Ou melhor, qual a fórmula do termo geral 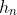 ?
?
Para responder a esta pergunta, vamos primeiro enumerar as subsequências  de acordo com o seu número de termos, da seguinte forma:
de acordo com o seu número de termos, da seguinte forma:
....................................
Assim, a posição  do termo genérico
do termo genérico 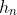 que finaliza uma subsequência em
que finaliza uma subsequência em  , é a soma dos índices de
, é a soma dos índices de  , ou seja
, ou seja
Logo, dado a posição  de
de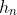 em
em  , temos que calcular
, temos que calcular  por intermédio de (1), que indicará em qual subsequência
por intermédio de (1), que indicará em qual subsequência 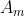 estará
estará 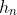 .
.
No entanto, pode acontecer que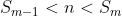 (a), no caso de
(a), no caso de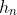 não finalizar uma subsequência
não finalizar uma subsequência 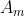 . Logo,
. Logo, 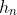 terá um valor entre o último termo de
terá um valor entre o último termo de ) e o último termo de
e o último termo de ) , ou seja,
, ou seja,
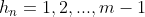
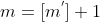
Suponhamos que que queremos calcular o termo de posição 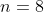 da sequência
da sequência  . Começamos indagando sobre o índice
. Começamos indagando sobre o índice  da subsequência
da subsequência  . Para isto, temos que enquadrar
. Para isto, temos que enquadrar 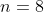 entre os números triangulares 1,3,6 e 10 que representam as somas dos índices de
entre os números triangulares 1,3,6 e 10 que representam as somas dos índices de  . Basta resolver a equação
. Basta resolver a equação
}{2}\Rightarrow%20m^2+m-16=0)
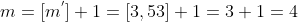
}{2}=\frac{4(4+1)}{2}=10)
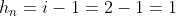
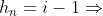
-1=n-b_1%20\Rightarrow)
%20\Rightarrow)
-(N+1))
 é fornecido;
é fornecido;
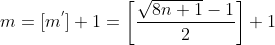 ; e
; e
}{2})
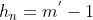 , com
, com

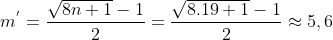
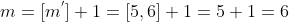
}{2}=\frac{6(6+1)}{2}=21)
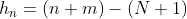
-(21+1)=25-22=3)
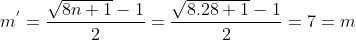
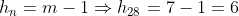
No entanto, pode acontecer que
Assim, resolvendo a equação (1) na variável  tendo em vista a condição (a) e sendo
tendo em vista a condição (a) e sendo  a raiz encontrada, consequentemente,
a raiz encontrada, consequentemente, 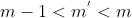 , de forma que
, de forma que 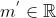 .
.
Se 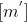 designar a parte inteira de
designar a parte inteira de  , então o índice da subsequência
, então o índice da subsequência 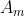 no qual se encontra
no qual se encontra 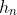 será
será
Veremos agora um exemplo esclarecedor. Observem a seguinte tabela:
cuja solução positiva é, aproximadamente,  . Logo,
. Logo,
e já sabemos que 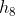 se encontra na quarta subsequência (
se encontra na quarta subsequência (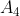 ).
).
Em seguida teremos que encontrar o índice  (última linha da tabela) de
(última linha da tabela) de 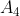 , tendo em vista que
, tendo em vista que 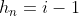 .
.
Seja 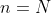 do termo de
do termo de  correspondente ao último termo da subsequência
correspondente ao último termo da subsequência 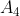 , ou seja,
, ou seja,
Assim, os quatro termos (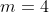 ) de
) de 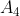 corresponderão aos índices
corresponderão aos índices  :
: 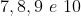 . Portanto,
. Portanto, 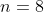 é referente a
é referente a  . Logo,
. Logo,
Podemos generalizar da sequinte forma.
O primeiro índice do termo de  que inicia a subsequência que contêm
que inicia a subsequência que contêm 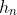 é
é 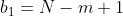 . De fato, pois
. De fato, pois  ;
;
O número  de termos que vai de
de termos que vai de 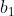 a
a  é
é 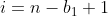 . Comprove:
. Comprove:  ;
;
E o enésimo termo de  é
é
onde,
Válido caso 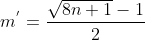 não seja um inteiro positivo. Caso seja, vale as fórmulas:
não seja um inteiro positivo. Caso seja, vale as fórmulas:
EXEMPLOS
1) Calcular 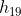 .
.
Resolução
2) Calcular 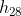 .
.
Resolução
_*_
Convido os leitores a resolverem os problemas do post 058 .
Gostará de ler também:
015-O Círculo Redutor e a Conjectura de Hunasses
058-O Problema dos Aviões e Outros Problemas/Questões
Gostará de ler também:
015-O Círculo Redutor e a Conjectura de Hunasses
058-O Problema dos Aviões e Outros Problemas/Questões


Olá Aloisio,
ResponderExcluirAgradeço por comentar esta sequência e colocar meu nome!
Como tinha dito antes para vc em outra ocasião,esta sequencia teve origem em outra.Eu queria achar a formula do termo geral da soma da serie harmônica:1+1/2+1/3+1/4+1/5+...+1/n.E numa certa oportunidade,transformei esta soma em:1+(1/4+1/4)+(1/9+1/9+1/9)+(1/16+1/16+1/16+1/16)+....+(1/n^2+1/n^2+...+1/n^2).A qtd de termos dentro do parênteses é n.
Então me fiz uma pergunta:É possível simplificar está soma para números mais simples?
Dai surgiu:1/2+1/2+1/3+1/3+1/3+1/4+1/4+1/4+1/4+....E se nao me falha a memória,a sequencia que vc comentou são restos de certa divisão.
Você lembra de onde vem?Mistério!!kkkk
Abraços.