Introdução
No post 047 vimos o teorema de Euler que afirma que, se =1) , então temos a equivalência
, então temos a equivalência ![a^{\varphi(m)} \equiv 1 [;a^{\varphi(m)} \equiv 1;]](http://thewe.net/tex/a%5E%7B%5Cvarphi%28m%29%7D%20%5Cequiv%201) (
(![mod [;mod;]](http://thewe.net/tex/mod)
![m [;m;]](http://thewe.net/tex/m) ), onde
), onde ) é a quantidade de inteiros positivos menores que/ e primos com
é a quantidade de inteiros positivos menores que/ e primos com 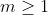 (função de Euler).
(função de Euler).
Seja a seguinte equação em 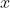 no conjunto universo
no conjunto universo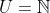 :
:
No caso 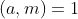 , o teorema de Euler já nos garante a solução
, o teorema de Euler já nos garante a solução ) , porém, ela não é única.
, porém, ela não é única.
É importante observar que a equação (1) terá soluções se, e somente se,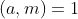 . De fato pois, sendo
. De fato pois, sendo 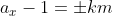 ou
ou 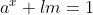 , temos que qualquer divisor comum de
, temos que qualquer divisor comum de  e
e 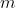 divide
divide 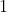 . Consequentemente,
. Consequentemente, 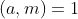 .
.
É importante observar que a equação (1) terá soluções se, e somente se,
O presente post tem, por intermédio da função expoente de  módulo
módulo 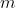 , o objetivo de elucidar a característica principal de todas as soluções de (1).
, o objetivo de elucidar a característica principal de todas as soluções de (1).
Nas demonstrações dos dois belos teoremas, nos apoiaremos também nos seguintes princípios:
Nas demonstrações dos dois belos teoremas, nos apoiaremos também nos seguintes princípios:
a) Todo subconjunto não vazio de inteiros não negativos possui um elemento mínimo ( Princípio da boa ordenação );
b) Dados os inteiros não nulos  e
e 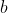 , temos que se
, temos que se  é múltiplo de
é múltiplo de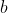 e
e 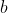 é múltiplo de
é múltiplo de  , então
, então 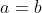 .
.
Definição de expoente de  módulo
módulo 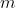
Dados
Teorema 1
Seja
Se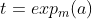 , então
, então
de forma que 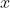 é múltiplo de
é múltiplo de 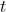 .
.
Demonstração
Seja
e como 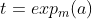 , por definição , é o menor elemento de
, por definição , é o menor elemento de 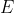 , segue que
, segue que
de forma que, para sustentar a equivalência (i) , é necessário ) . Portanto,
. Portanto,  . Lembrem-se que
. Lembrem-se que  . Mas pelo princípio a) ,o conjunto
. Mas pelo princípio a) ,o conjunto 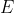 tem um elemento mínimo e já sabemos que é
tem um elemento mínimo e já sabemos que é 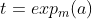 . Logo,
. Logo, 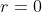 e
e  e está provado que qualquer solução de
e está provado que qualquer solução de 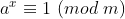 é múltiplo de
é múltiplo de 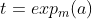 .
.
Teorema 2
Dados
Demonstração
Fazendo ) e tendo em vista que
e tendo em vista que ) , temos
, temos
Pelo teorema  ,
,  é múltiplo de
é múltiplo de  .
.
Pelo mesmo teorema, de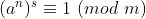 , temos que
, temos que  é múltiplo de
é múltiplo de 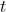 .
.
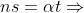
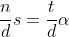
=\frac{t}{(n,t)})
Gostará de ler também:
048-Fundamentos de Congruência Modular
046-Critérios de Divisibilidade
055-Cálculo de Resto sem Dividir
047-Teoremas de Euler e Fermat
049-Equação de Congruência Linear
050-Equação de Congruência Polinomial
051-Teorema de Wilson-II
Pelo mesmo teorema, de
Assim, para algum 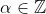 :
:
e fica claro que  divide
divide 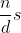 . Mas, como
. Mas, como ) segue que
segue que =1) e, portanto,
e, portanto,  divide
divide  ou
ou  é múltiplo de
é múltiplo de  . Ora, mas sabemos logo no início da demonstração que
. Ora, mas sabemos logo no início da demonstração que 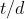 é múltiplo de
é múltiplo de  . Logo, pelo princípio b) , concluimos que
. Logo, pelo princípio b) , concluimos que
Gostará de ler também:
048-Fundamentos de Congruência Modular
046-Critérios de Divisibilidade
055-Cálculo de Resto sem Dividir
047-Teoremas de Euler e Fermat
049-Equação de Congruência Linear
050-Equação de Congruência Polinomial
051-Teorema de Wilson-II



Olá Aloisio, gostaria de parabenizar pela qualidade do seu blog! Você aborda temas interessantes com clareza... Quanto a este post, particularmente, estive pensando sobre ele e gostaria que você considerasse o seguinte:
ResponderExcluirUsando a notação "a -= b(mod c)" para "a congruente b módulo c", "\in" para pertinência, o conjunto E como você definiu no Teorema 1 e N o conjunto dos Naturais.
P1. Se existe t \in N, tal que t é uma solução particular de a^x -= 1(mod m), então E = N.
Prova:
Se t = 1, então, pelo Teorema 1, não há o que ser provado. Vamos assumir t <> 1, assim,
a -= r(mod m), r \in Z\{1} e a^t -= 1(mod m).
Seja a^(t-1) -= s(mod m), s \in Z, temos que
a -= r(mod m)
a^(t-1) -= s(mod m)
a * a^(t-1) -= r*s(mod m)
a^t -= r*s(mod m)
Desse modo,
r*s = 1
Como r e s são números inteiros,logo r = s = 1, mostrando que x = 1 também é solução de a^x -= 1(mod m) e E = N. QED
Você concorda?
Oi, Daniel!
ResponderExcluirObrigado pelo demonstração de apreço.
Sobre sua prova, acho que cometeu um pequeno deslize, mas acredite, é muito comum.
A propriedade transitiva da aritmética modular diz que se A -=B e B-=C, então A-=C (tudo mod m), mas não necessáriamente A=C.
Vc fez o seguinte, pelo que entendi:
Se r*s-=a^t e a^t-=1, então r*s=1 (tudo mod m)
Mas o correto é apenas concluir que r*s-=1(mod m).
Valeu, um grande abraço!