Tipo
Sobre o período destas funções, podemos dizer que:
a) 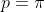 , se
, se 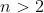 for par;
for par;
b) 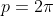 , se
, se  for ímpar.
for ímpar.
Considerações gerais sobre o gráfico da função definida por
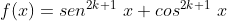 , para
, para 
Intersecção com os eixos coordenados
Intersecção com os eixos coordenados
Colocando os gráficos de 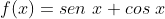 e
e 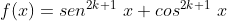
) em um mesmo sistema de coordenadas ortogonais, podemos ter uma idéia inicial das principais semelhanças e diferenças entre estas funções. Observem.
em um mesmo sistema de coordenadas ortogonais, podemos ter uma idéia inicial das principais semelhanças e diferenças entre estas funções. Observem.
À primeira vista, estas equações possuem as mesmas raízes ou zeros. Além disso, as duas curvas interceptam o eixo
Sobre as raízes,vejam que
e provamos que as duas equações em estudo possuem de fato, as mesmas raízes. Pelo post 87 sabemos que estas raízes são
Já o ponto de intersecção com o eixo 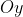 terá abcissa
terá abcissa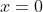 e ordenada
e ordenada
=sen^{2k+1}%20\%200%20+cos^{2k+1}%20\%200=0+1=1)
Resumindo graficamente o que vimos até agora:
Pontos críticos de
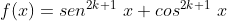
)
Quando
Logo, dado 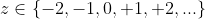 se verificará a derivada
se verificará a derivada 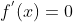 toda vez que
toda vez que
Selecionando as seguintes abcissas dos pontos críticos que estão limitadas em um período, temos
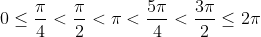
=1)
=sen^{2k+1}\left(\frac{\pi}{4}\right)+cos^{2k+1}\left(\frac{\pi}{4}\right)=\left(\frac{\sqrt{2}}{2}\right)^{2k+1}%20+\left(\frac{\sqrt{2}}{2}\right)^{2k+1}=\frac{\sqrt{2}}{2^k})
=sen^{2k+1}\left(\frac{\pi}{2}\right)+cos^{2k+1}\left(\frac{\pi}{2}\right)=1^{2k+1}+0^{2k+1}=1)
=sen^{2k+1}%20\%20\pi+cos^{2k+1}%20\%20\pi=0^{2k+1}+(-1)^{2k+1}=-1)
=sen^{2k+1}\left(\frac{5\pi}{4}\right)+cos^{2k+1}\left(\frac{5\pi}{4}\right)=\left(-\frac{\sqrt{2}}{2}\right)^{2k+1}+\left(-\frac{\sqrt{2}}{2}\right)^{2k+1}=-\frac{\sqrt{2}}{2^k})
=sen^{2k+1}\left(\frac{3\pi}{2}\right)+cos^{2k+1}\left(\frac{3\pi}{2}\right)=(-1)^{2k+1}+0^{2k+1}=-1)
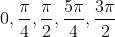
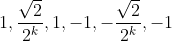
Assim,
Logo, para valores de  (onde a derivada é zero ) iguais à
(onde a derivada é zero ) iguais à
temos valores de  iguais a
iguais a
respectivamente, que são as ordenadas dos pontos críticos da função no intervalo em uma primeira repetição desta sequência. Segue o esboço do gráfico.
em uma primeira repetição desta sequência. Segue o esboço do gráfico.
De forma que a imagem desta função é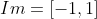 .
.
De forma que a imagem desta função é
Evolução da função
=sen^n%20\%20x+cos^n%20\%20x)
para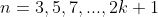
para
Se  tender para o infinito, ou seja,
tender para o infinito, ou seja, 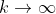 , teremos pontos limites periódicos de pontos críticos, todos contidos no eixo
, teremos pontos limites periódicos de pontos críticos, todos contidos no eixo 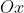 , tomando como exemplo, os dois seguintes no intervalo
, tomando como exemplo, os dois seguintes no intervalo 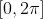 :
:
=\left(\frac{\pi}{4},0%20\right%20))
=\left(\frac{5\pi}{4},0%20\right%20))
087-Estudo da Função f(x)=sen x +cos x
028-Gráficos Cartesianos Algébricos
042-Área de Intersecção Circular-Raios Iguais
Referência bibliográfica:
-Fundamentos de Matemática Elementar V1-Conjuntos-Funções, Atual Editora, ;
;
-Fundamentos de Matemática Elementar V4-Trigonometria, Atual Editora, .
.
Desta forma, quanto maior for  ímpar
ímpar 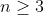 ,os pontos críticos para as abcissas dos tipos
,os pontos críticos para as abcissas dos tipos 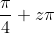 e
e 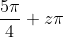 tenderão a aproximar-se do eixo
tenderão a aproximar-se do eixo 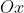 , sem interceptá-lo. Veja o diagrama.
, sem interceptá-lo. Veja o diagrama.
Gostará de ler também:
087-Estudo da Função f(x)=sen x +cos x
028-Gráficos Cartesianos Algébricos
042-Área de Intersecção Circular-Raios Iguais
Referência bibliográfica:
-Fundamentos de Matemática Elementar V1-Conjuntos-Funções, Atual Editora,
-Fundamentos de Matemática Elementar V4-Trigonometria, Atual Editora,









Olá, Aloísio!!!!
ResponderExcluirParabéns!!!! Ótima postagem e... parece que você estava adivinhando que eu precisava dessas informações para desenvolver os módulos de aplicações do meu algoritmo!!!! Muito bom e... sorte minha, pois, aqui está tudo explicado, do modo como eu queria!!!! Muito bom!!!!
Mas, eu pergunto: vai ajudar ao Superman ou não vai???? Salvem a Terra, rsrsrsrs, da ameaça bizarra!!!!
Um abraço!!!!!
Oi, Valdir!
ResponderExcluirFico contente que tenha gostado. E ainda mais por ter colaborado com o seu algoritmo.
O mérito de estudar estas funções é que, quem o faz, recorda e exercita os conhecimentos trigonométricos. É uma maneira interessante de estudar. Por exemplo, a função f(x)=sen (x^2).
O Superman está pedindo ajuda??? Quem sou eu!!!??? rsrs Mas pode deixar que vou tentar resolver o seu desafio, Valdir.
Outro abraço e até mais!