No presente artigo, mostraremos de que forma podemos deduzir as referidas fórmulas por intermédio da forma polar do número complexo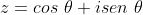 
e do binômio de Newton ^n "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
.
O que queremos é expressar  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
e  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
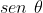em termos de 
e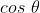 
.
Usaremos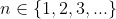 
. Conforme a fórmula de Moivre ( demonstrada no post 081 ), temos
^n "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
(1)
+isen(n\theta) "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
(2)
^n=\sum_{p=0}^{n}{n%20\choose%20p}cos^{n-p}%20\theta.i^p.sen^p%20\theta "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
={3%20\choose%200}cos^3%20\theta%20\%20sen^0%20\theta-{3%20\choose%202}cos^1%20\theta%20\%20sen^2%20\theta%20\Rightarrow "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
=cos^3%20\theta-3cos%20\theta%20\%20sen^2%20\theta "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
={4%20\choose%200}cos^4\theta%20sen^0%20\theta-{4%20\choose%202}cos^2\theta%20sen^2%20\theta+{4%20\choose%204}cos^0\theta%20sen^4%20\theta%20\Rightarrow "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
=cos^4\theta-6cos^2\theta%20sen^2%20\theta+sen^4%20\theta "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
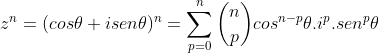
={3%20\choose%201}cos^2\theta%20sen^1%20\theta-{3%20\choose%203}cos^0\theta%20sen^3%20\theta%20\Rightarrow "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
=3cos^2\theta%20sen%20\%20\theta-sen^3%20\theta "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
={4%20\choose%201}cos^3%20\theta%20\%20sen^1\theta-{4%20\choose%203}cos^1%20\theta%20\%20sen^3\theta%20\Rightarrow "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
=4cos^3%20\theta%20\%20sen%20\%20\theta-4cos%20\%20\theta%20\%20sen^3\theta "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
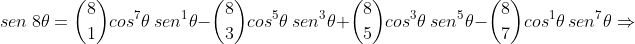
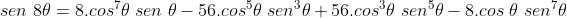
Podemos, então, desenvolver (1) pelo binômio de Newton, separar as partes real e imaginária do resultado e comparar com (2), obtendo as expressões para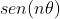 
e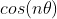 
.
Na síntese da expansão binomial , temos
Os termos de 
que compõe sua parte real são aqueles onde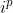 
é real, ou seja, para 
, 
, 
, 
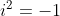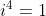, etc. Logo, neste caso, 
, que também é a potência do seno, é par. Já temos como calcular . Vejamos alguns exemplos.
Reparem que as potências do seno são pares e os sinais dos termos alternam devido a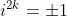 
, com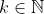 
.
Observando novamente a identidade
notamos que os termos de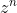 
que compõe sua parte imaginária são aqueles onde 
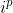é complexo, ou seja, para 
, 
, 
, 
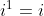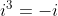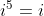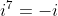, etc. Logo, neste caso, , que também é a potência do seno, é ímpar. Já temos como calcular . Vejamos alguns exemplos.
Observem que as potências do seno são ímpares e os sinais dos termos alternam devido a ![[;i^{2k+1}=\pm i;]](http://thewe.net/tex/i^{2k+1}=\pm i "i^{2k+1}=\pm i")
, com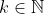 
.
Aplicação. A equação polar da rosácea de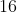 
pétalas é 
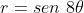. Qual é a equação desta curva em coordenadas retangulares?
Para transformar uma equação polar em retangular, basta substituir 
, 
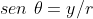e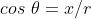 
. Mas antes, temos que desenvolver 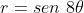em termos d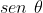e e 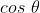. Conforme a fórmula para seno de ângulo múltiplo, temos
Assim,
que é a equação para coordenadas retangulares da rosácea de 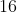pétalas.
Observem como esta teoria se harmoniza com as fórmulas conhecidas de arco duplo:
![[;sen \ 2 \theta={ 2 \choose 1}cos^1 \theta sen^1 \theta=2sen \ \theta.cos \ \theta;]](http://thewe.net/tex/sen \ 2 \theta={ 2 \choose 1}cos^1 \theta sen^1 \theta=2sen \ \theta.cos \ \theta "sen \ 2 \theta={ 2 \choose 1}cos^1 \theta sen^1 \theta=2sen \ \theta.cos \ \theta")
Observem como esta teoria se harmoniza com as fórmulas conhecidas de arco duplo:
Muito boa esta ligação entre duas áreas distintas da Matemática. Se primeiros matemáticos a estudar os números complexos estivessem interessados apenas nas aplicações, esta teoria nunca teria desenvolvido ao ponto de colher os frutos das aplicações. Este artigo mostra que o estudo por si só de uma teoria matemática é muito gratificante.
ResponderExcluirOi, Paulo!
ExcluirObrigado pela inspiração do post.
Os antes rejeitados números complexos são de uma importância fundamental hoje em dia. Deveriam até mudar de nome. Eles se encaixam na trigonometria como se fossem criados para isto. Aqui temos também a ligação com a teoria do binômio de Newton.