Teorema. Seja um ponto
Demonstração. O ângulo 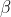 é formado entre duas perpendiculares consecutivas (
é formado entre duas perpendiculares consecutivas (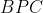 ,
, 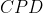 , etc...). Assim, a soma de todos os ângulos
, etc...). Assim, a soma de todos os ângulos 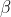 é
é 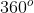 , ou seja,
, ou seja, 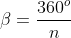 .
.
Em relação à segunda perpendicular ![PC [;PC;]](https://thewe.net/tex/PC) :
:
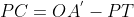 ,com
,com
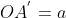
e
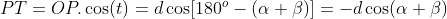
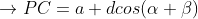
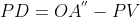 , com
, com
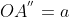
e
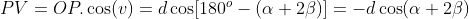
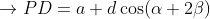
e
Em relação à terceira perpendicular 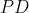 :
:
e
E assim por diante, de forma que
Primeira perpendicular: 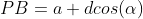
Segunda perpendicular: 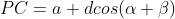
Terceira perpendicular: 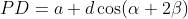
Quarta perpendicular: 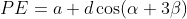
Enésima perpendicular: 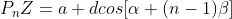
Logo, a soma das perpendiculares será
E a soma  dos segmentos perpendiculares fica
dos segmentos perpendiculares fica
Finalmente, como ![\beta=\frac{360^o}{n} [;\beta=\frac{360^o}{n};]](https://thewe.net/tex/%5Cbeta=%5Cfrac%7B360%5Eo%7D%7Bn%7D) , o fator
, o fator ![sen \left(\frac{\beta n}{2}\right) [;sen \left(\frac{\beta n}{2}\right);]](https://thewe.net/tex/sen%20%5Cleft%28%5Cfrac%7B%5Cbeta%20n%7D%7B2%7D%5Cright%29) entre chaves do numerador é igual a
entre chaves do numerador é igual a![sen \left(\frac{360^o}{n}.\frac{n}{2}\right)=sen(180^o)=0 [;sen \left(\frac{360^o}{n}.\frac{n}{2}\right)=sen(180^o)=0;]](https://thewe.net/tex/sen%20%5Cleft%28%5Cfrac%7B360%5Eo%7D%7Bn%7D.%5Cfrac%7Bn%7D%7B2%7D%5Cright%29=sen%28180%5Eo%29=0) .
.
Logo, ![S=n.a [;S=n.a;]](https://thewe.net/tex/S=n.a)
 Nota Histórica: Vicenzo Viviani (
Nota Histórica: Vicenzo Viviani (![1622-1703 [;1622-1703;]](https://thewe.net/tex/1622-1703) ) , matemático e cientista italiano, foi aluno de Evangelista Torricelli (
) , matemático e cientista italiano, foi aluno de Evangelista Torricelli (![1608-1647 [;1608-1647;]](https://thewe.net/tex/1608-1647) ) e, durante um bom período, colaborador direto de Galileu Galilei (
) e, durante um bom período, colaborador direto de Galileu Galilei (![1564-1642 [;1564-1642;]](https://thewe.net/tex/1564-1642) ). Quando este morreu, Viviane foi seu biógrafo. A reputação de grande filósofo natural que Vicenzo tinha na época, começou a ser destruída quando a Igreja o proibiu de publicar uma edição completa das obras de Galileu. Publicou a versão italiana dos Elementos de Euclides em
). Quando este morreu, Viviane foi seu biógrafo. A reputação de grande filósofo natural que Vicenzo tinha na época, começou a ser destruída quando a Igreja o proibiu de publicar uma edição completa das obras de Galileu. Publicou a versão italiana dos Elementos de Euclides em ![1690 [;1690;]](https://thewe.net/tex/1690) . O teorema de Viviani é o caso particular do presente teorema quando o número de lados do polígono regular é
. O teorema de Viviani é o caso particular do presente teorema quando o número de lados do polígono regular é ![n=3 [;n=3;]](https://thewe.net/tex/n=3) ( triângulo equilátero, onde a altura é o triplo da apótema ).
( triângulo equilátero, onde a altura é o triplo da apótema ).
 Nota Histórica: Vicenzo Viviani (
Nota Histórica: Vicenzo Viviani (
Referência Bibliográfica
Trigonometria Elementar, F.T.D, Ed.Livraria Paulo Azevedo & Cia, 1928.
O Livro da Matemática, Clifford A. Pickover, Ed.Librero, 2009.
Imagens
http://pt.wikipedia.org/wiki/Vincenzo_Viviani





Excelente post. Bastante elegante a demonstração. Nunca tinha ouvido falado desse teorema. Permita-me dar outra solução (sempre bom ter mais de uma):
ResponderExcluirSeja S a área do poligono citado ( com n lados de comprimento l ). Temos:
S=(PA.l+PB.l+...+PZ.l)/2=n{OA.l}/2
Segue que:
PA.l+PB.l+...+PZ.l=nOA.l.
Logo,
PA+PB+...+PZ=n.OA.
Obrigado, Hugocito! E, de fato, sua demonstração é mais simples. Mas neste artigo encontrei uma boa oportunidade para aplicar os somatórios trigonométricos. A demonstração que apresentei encontrei em um livro impresso em 1928! Valeu.
ResponderExcluirOs livros antigos são os melhores. Eu tenho alguns.
ResponderExcluirSemprei estudei com eles e não me arrependo.
Veja que coisa interessante.
ResponderExcluirVocê mostrou que
S=na+d[cos(alfa)+...+cos(alfa + (n-1)beta)]
e eu mostrei que S=na.
Logo, temos uma demonstração geométrica de que
cos(alfa)+...+cos(alfa + (n-1)beta)=0.
Ou seja, combinando esses métodos de demonstração, temos uma demonstração simples desse somatório
Bem interessante este teorema. Eu conhecia apenas um problema semelhante no triângulo equilátero cuja demonstração é igual a apresentada pelo Hugocito. Combinando resultados, temos uma prova geométrica da integral natural ou antiderivada finita da sequência cosseno.
ResponderExcluirTem também o curioso teorema de Morley ([;1860-1937;]) que diz que, em qualquer triângulo, os três pontos de intersecção das trissetrizes adjacentes formam sempre um triângulo equilátero. Este teorema foi demonstrado rigorosamente apenas no século [;XX;], mas desconheço a prova.
ResponderExcluirTem a demonstração em Coxeter and Greitzer - Geometry Revisited (1967).
ResponderExcluirPágina 47.
Caso não tenha o livro, baixe ele pelo link:
http://analgeomatica.files.wordpress.com/2008/11/geometryrevisited_coxetergreitzer_0883856190.pdf
Faz uma postagem sobre ele, é interessante e desconhecido.
Oi, Hugocito!
ResponderExcluirPena que seja em inglês. Eu não domino a língua inglesa.
Acho que vc é o mais qualificado para fazer a postagem.
Abraços!
Vou tentar fazer nos proximos dias então.
ExcluirAxei uma demonstração em portugues. Tem duas demonstrações.
Excluirhttp://www.atractor.pt/mat/morley/index.htm
Daora, tem até as generalizações. Muito daora.
ExcluirMuito bacana, Hugocito!
ExcluirAgora vc pode fazer a postagem.
Excluir(=