Se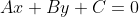 
é a equação geral de uma reta 
e  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
é um ponto qualquer do plano, então a distância ortogonal de 
à é dada pela elegante fórmula
Por exemplo, se queremos a saber a distância do ponto  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
à reta gerada pela equação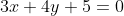
, basta fazer
DEMONSTRAÇÃO
Observem o diagrama. Nosso objetivo é calcular a distância 
do ponto dado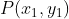
à reta fornecida pela equação .
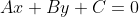Utilizaremos, por ser mais prático neste caso, a equação reduzida da reta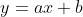 
, com 
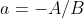e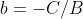 
.
Considere o segmento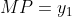 
que intercepta a reta no ponto 
de coordenadas "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
. Assim,
pois estando na reta dada, suas coordenadas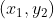 
satisfazem a equação .
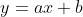No triângulo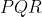 
, temos 
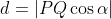. Mas,
Finalmente, retornando com os valores 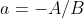e 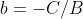chegamos à
_*_
O matemático italiano Joseph Lagrange  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
foi o primeiro a provar que a distância de um ponto  "This is the rendered form of the equation. You can not edit this directly. Right click will give you the option to save the image, and in most browsers you can drag the image onto your desktop or another program.")
ao plano de equação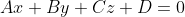 
é
_*_
Referência Bibliográfica:
-Matemática-Terceiro Ano Colegial, Ary Quintella, Companhia Editora Nacional, São Paulo, 
;
- História da Matemática , Carl B.Boyer, Editora Edgard Blücher LTDA, 
.
Interessante a abordagem feita para deduzir a distância de um ponto a uma reta, pois envolvem conceitos de geometria analítica e trigonometria. Para complementar o seu post, apresento outra forma de deduzir esta expressão neste link http://fatosmatematicos.blogspot.com.br/2009/08/distancia-de-de-ponto-reta.html
ResponderExcluirOi, Paulo!
ExcluirAchei legal a "prova sem palavras". Já inclui no texto.
Obrigado pela sugestão.
Até mais!
Olá,nossa adoro esse blog,só tem artigo bom,sempre que dá estou passando aqui,depois que meu amigo me recomendo nunca mais deixei de visitar,alguem sabe me falar se assim aqui é bom www.softwarecelularespiao.org ? abraços,assim que der eu volto pra comentar aqui no blog
ResponderExcluirElegante!
ResponderExcluirEstimas!